Bonjour j'ai besoin d'aide pour une question :
iii) on suppose que m>0 et que n n'est pas le produit de m par un entier impair. Montrer qu'il existe un unique entier p>=1 tel que abs(n-2m)<m et que:
Qn,m=2(Tn,m-Tn,3m+...+(-1)^(p-1)Tn-(2p-1)m) et Rn,m=(-1)^(p)T(abs(n-2pm)
Normalement le peut etre trouvé sur internet en tapant centrale polynome de tchebychev dans la partie division euclidienne .Merci!!
Polynome de tchebychev
3 messages
- Page 1 sur 1
Re: Polynome de tchebychev
Considère  le plus grand élément de l'ensemble
le plus grand élément de l'ensemble 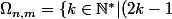m<n\}) , je te laisse justifier que ce que je dis a du sens.
, je te laisse justifier que ce que je dis a du sens. m}=T_{n-2km}+T_{n-(2k+2)m}) , en multipliant par
, en multipliant par ^k) tu peux sommer et avoir une somme télescopique.
tu peux sommer et avoir une somme télescopique.
Re: Polynome de tchebychev
J'ai reussi au debut en majorant par part.ent(((n/m+1)/2)+ puis grace aux sommes telescopique j'ai trouvé la somme mais je me retrouve avec Tn-2(p-1)m(-1)^(p-1) et je n'arrive pas à montrer que c'est egal à 2Tn-(2p-1)m -Tabs(n-2pm) .Comment faire?
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
