Polynôme - Fonction symétrique élémentaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 19 Fév 2014, 11:40
par Charmander » 19 Fév 2014, 11:40
Bonjour,
Soit P un polynôme de degré n à coefficients complexes, et
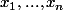
ses racines.
Dans les exercices préliminaires, on a démontré que pour tout

et
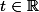
:
}{P(t)} = \sum_{i=1}^{N} \frac{(S_k)^{i-1}}{t^i} + o(\frac{1}{t^N}))
au voisinage de

avec
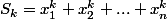
pour tout k
Voici l'énoncé de l'exercice :
On considère n=3.
Déduire du développement limité les relations :
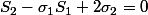
et

avec
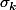
la fonction symétrique élémentaire
 = \sum_{1\leq i_1<...< i_k\leq n} x_{i_1} x_{i_2}...x_{i_k})
J'ai pour indice :
multiplier le développement par P(t)J'ai beau essayer, je ne vois pas comment faire... Substituer la racine après avoir multiplié par P(t) ne mène à rien.. Quelqu'un pourrait m'aider please ? Merci d'avance...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Fév 2014, 13:17
par Doraki » 19 Fév 2014, 13:17
Tu écris P(t) et P'(t) en fonction de ;)1,;)2,;)3, puis tu écris que P(t) * (P'(t)/P(t)) = P'(t)
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 19 Fév 2014, 15:09
par Charmander » 19 Fév 2014, 15:09
Doraki a écrit:Tu écris P(t) et P'(t) en fonction de

1,;)2,;)3, puis tu écris que P(t) * (P'(t)/P(t)) = P'(t)
Juste pour en être sûr, au degré 3 on a
 = a_n (t^3-\sigma_1 t^2 + \sigma_2 t - \sigma_3 ))
?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Fév 2014, 20:14
par Doraki » 19 Fév 2014, 20:14
oui. Maintenant tu dérives pour avoir P' et puis tu fais la multiplication.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
et

la fonction symétrique élémentaire
