Petite queston "lim inf"

[simplet]

Bonjour,

Soit (fn) une suite de fonctions d'indice n.

j'aurais voulu qu'on m'explique l'écriture "(lim inf fn) quand n tend vers l'infini".

Est-ce que c'est la limite de l' "inf fn" quand n tend vers l'infini? Ce qui m'intrigue alors, c'est que le "inf fn" n'est déjà pas une limite? laquelle sera la borne infèrieure des fn quand n parcours l'ensemble des naturels?

Ca parait bête mais je me mélange un peu les pinceaux...

merci
simplet

[Anonyme]

bah , si inf (fn)=f1 (par exemple)
que signifie lim(f1) quand n tend vers l'infini??

comprend pas non plus :-)

[Yipee]

La question n'est pas très claire. L'énoncé semble suggérer que tu regardes, la limite des nombres a_n = Inf(f_n) où l'Inf est prise sur un ensemble qui n'est pas précisé.

Cependant, on peut aussi imaginer qu'il s'agit vraiment d'une "lim inf". A savoir que tu considères tes fonctions comme éléments d'un ensemble normé. Alors tu peux prendre la lim inf des nombres b_n = norme(f_n). A ce moment, on note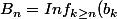 . A ce moment
la lim inf est la limite des B_n.

[simplet]

En fait pour faire simple, disons que je n'arrive pas à me représenter ce qu'est (pour la suite (fn) ) la limite quand n tend vers l'infini de inf(fn) ?

Intuitivement, qu'est-ce que ca représente??

merci

[El_Gato]

Non non, la limite inf ce n'est pas la limite des inf. C'est une nouvelle notion de limite, plus faible, mais plus maniable que la notion de limite habituelle.

Si (fn) est ta suite de fonctions, tu considères pour k = 1, 2, ... la suite de fonctions gk définie par:

gk = Inf fn, pour n >= k (k fixé).

Tu vois tout de suite que g1 <= g2 <= g3 <= ...

La suite gk croit, donc elle admet une limite (éventuellement infinie) g, qui n'est autre que le sup des gk. Cette limite s'appelle la lim inf de la suite fn: c'est le "sup des inf".

L'intérêt de cette notion: la limite inf existe toujours. Et si la suite fn converge (au sens habituel) la limite est égale à la limite inf.

On définit de même la limite sup.

Ainsi, si tu as une suite de fonctions fn, tu peux tout de suite écrire: "considérons lim inf fn" alors que pour la limite au sens habituel, il faut d'abord démontrer qu'elle existe.

D'où l'intérêt énorme de cette notion.

Pour voir ce que cela représente, ça n'est pas difficile: lim inf fn (x) est la plus petite valeur d'adhérence des fn(x).

[simplet]

merci beaucoup,
il est vrai que les livres ne prennent pas assez le temps d'expliquer cette notation, d'où ma question. encore merci