Partition d'un ensemble

[mehdi-128]

Bonjour,

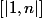
Soient E et F 2 ensembles de cardinal fini. Ils sont donc en bijection avec et .

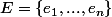
Posons : et

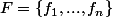
Notons l'ensemble

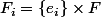
Je cherche à montrer que : est une partition de

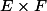
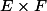
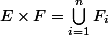
1/ Je dois montrer que la réunion des est bien égale à car : . Je vois pas comment faire.

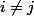
2/ Je dois montrer que pour on a :
Je vois pas trop non plus.

3/ Je dois montrer que chacune des pour i allant de 1 à n est :
Je vois pas trop non plus.

Merci d'avance.

[pascal16]

tu cherches trop compliqué.
C'est pas de la rédaction très 'supérieur' :

Fi= ei X F
ei, non nul car {e1,..ei, en} est une partition d’éléments de E et n >=1
si F est non vide, {ei} X F est non vide (on peut même accepter F vide).


pour les question 1 et 2, part d'un exemple :
exemple E={1,2,3}
F= { rouge, vert}

F1={(1,Rouge),(1,vert)}
F2={(2,Rouge),(2,vert)}
F3={(3,Rouge),(3,vert)}
est-ce que j'ai bien tous les couples du type (un élément de E, un élément de F)= ExF ?
est-ce que j'ai un couple cité deux fois ?

[mehdi-128]

J'ai compris votre exemple, oui on a tout les éléments de E x F.

Du coup j'ai rien à démontrer pour dire que c'est une partition ? Faut juste le remarquer ?

[hdci]

Non, "juste remarquer" ne suffit pas sauf lorsque le sujet est "trivialement évident", mais "trivialement évident" dépend énormément du niveau et ici m'est avis qu'il faut détailler un peu.

Trois points pour une partition : la réunion fait le tout, les parties sont disjointes deux à deux et aucune n'est vide (encore que selon les définitions cette dernière condition peut être omise).

La réunion fait le tout : il suffit de s'assurer qu'un élément quelconque est dans au moins l'un des .

• Or pour un certain et un certain
• et par définition

Disjoints deux à deux : donc si alors .

• Or les éléments de sont de la forme
• et si alors on a ce qui est impossible si .

Aucun des ensembles n'est vide : il suffit d'exhiber un élément pour chaque

• par exemple

[pascal16]

Voilà, c'est maintenant un exemple compréhensible et une rédaction propre

[LB2]

Bonjour,

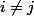
2/ Je dois montrer que pour on a :

Merci d'avance.

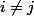
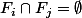
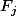
Non, tu dois montrer que pour on a : , ce qui est très différent. On dit que et n'ont aucun élément en commun, ou encore qu'ils sont disjoints.

L'idée derrière ton exercice est en fait très simple. Si tu représentes les éléments de ExF dans un tableau à n lignes et m colonnes, par exemple, à quoi correspondent tes ensembles , , , .... ?

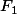
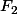
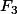
Et vois-tu comment faire une autre partition (en inversant le rôle de E et F) ?

Cordialement

[mehdi-128]

@hdci

Merci beaucoup super clair !

Juste un petit détail pour le premier point, on doit montrer que la réunion fait le tout.

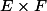
Vous êtes parti d'un élément de et vous avez montré qu'il appartient à l'un des
Faut aussi faire l'inclusion inverse non ? L'union des doit être incluse dans

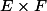
[hdci]

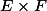
En partant d'un élément de on montre qu'il appartient à l'un des .

Cela montre qu'effectivement

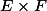
L'inclusion inverse est triviale puisque les éléments des sont forcément dans , par définition même des .

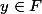
S'il faut le faire "très formellement" il suffit de remarquer que puisque si , alors et , donc .
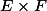
Alors, chaque étant inclus dans , leur réunion l'est forcément.