Dante0 a écrit:C'est le "engendré" qui me pose un soucis, ca a un rapport avec les espaces vectoriels ?
ça ce voit que tu ne lis pas ton cours, tout ça ce sont des questions du cours, tu dois commencer par revoir ton cours depuis le début, paragraphe par paragraphe, et tu verras que c'est très simple. Si tu es encore juste au début du cours, attend le moment où tu arriveras dans ton cours au paragraphe qui porte sur les tribu engendré par une partie de sous ensemble. c'est dans les premiers chapitres du cours. et ce n'est pas difficile.
Concernant ta question :
Si

est un espace et

est une partie de
)
( C'est très important de comprendre ce que signifie

est une partie ( ou classe ) de
)
. Alors
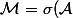)
est la tribu engendré par

signifie que

:

s'exprime en fonction d'éléments de

à l'aide des trois opérations

. Par exemple :
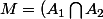 \backslash ( A_1 \bigcap A_2 ))
, avec :

. C'est juste un exemple, il y'en a plusieurs.
La partie

de
)
peut être une tribu si et seulement si :
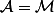
Donc, tu peux constater que toute tribu est une partie de
)
, par contre toute partie de
)
peut ne pas être une tribu.
Toute partition :

est une partie de
)
, mais elle n'est pas une tribu, comme

, qu'on a consideré qu'elle n'est pas une tribu, mais on peut construire la tribu engendré par cette partition
)
.
Exemple de tribu engendré par une partition :
 = \{ E , A , A^c , \emptyset \} \subset \mathcal{P} ( \Omega ))
avec

.
Cordialement.
