Partie fractionnaire d'une suite

[Pavel]

Bonjour à tous

J'ai qques difficultés avec l'exercice suivant :

Un est une suite réelle qui tend vers + infini et
Un+1 - Un tend vers 0

Mq {Un - E(Un)|n dans N} est dense dans [0,1].

Ca parait intuitif, mais je sais pas comment l'écrire.

Merci d'avance pour votre aide

[Isomorphisme]

Bonjour,

Si on note :
on sait déjà que , en effet, il est évident que (il suffit d'utiliser la définition de la partie entière)
Or il est évident que que la fermeture de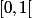 est .
Il faut à présent montrer que converge. il suffit de montrer qu'elle est de Cauchy, ce qui est évident étant donné que converge.

[Pavel]

Je suis d'accord avec ce que tu as écrit, mais je vois pas pkoi A est dense dans [0,1].

[Isomorphisme]

Un ensemble est dense dans un ensemble si la fermeture de relativement à est (il existe d'autres définitions de la densité : il suffit de montrer que pour tout élément de il existe une suite d'éléments de qui converge vers