Bonjour à tous ,
Je suis en 3ème année de licence MIASHS, j'ai un dm à rendre et je ne comprends quasiment rien. J'ai vraiment beaucoup de mal depuis le début de l'année.
1. Soit la fonction f définie sur R2 par X = (x,y) → f(X) = exp(x−y) − (1 + x + y).
(a) Sur quelle courbe de niveau de f se situe X0 = (0,0)? On notera cette courbe Nf(0) par la suite.
(b) Donner les expressions de ∂f / ∂x (X) et de ∂f / ∂y (X).
Calculer ∂f / ∂x (X0) et ∂f / ∂x (X0).
(c) Montrer qu’il existe des intervalles I et J centrés en 0 tels que pour tout x ∈ I, il existe un unique ϕ(x) ∈ J tel que f(x,y) = 0.
(d) Donner les expressions de ϕ′(x) et de ϕ′′(x). Calculer leur valeur en 0.
Je pense avoir réussit ces 4 premières questions.
Pour la (a) j'ai rempplcé x et y par 0
Pour la (b) j'ai calculer les derivées partielles, puis ensuite en remplacant par 0
Pour la (c) et ma (d) j'ai utilisé le Théorème des fonctions implicites.
Et après je n'y arrive plus :
(e) Vérifier que le gradient de f en X0 est orthogonal à la droite tangente à Nf(0) en X0.
Et là je ne vois pas du tout comment faire ...
Merci d'avance.
Optimisation (gradient, courbe de niveau)
2 messages
- Page 1 sur 1
Re: Optimisation (gradient, courbe de niveau)
Salut, tu as tout pour trouver le gradient grâce à 1b et ensuite tu peux écrire un développement limité pour obtenir l'expression de ta tangente ( à justifier); (x,y) appartient à Nf(à) équivaut à exp(x-y) -(1+x+y) = 0 soit
1+(x-y) +o(x-y) -(1+x+y) = 0 soit y=....
Tu as donc un vecteur directeur de ta tangente et tu vérifies que le gradient est bien orthogonal.
{à vérifier!!!}
Tu peux aussi utiliser ,
, 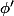 pour trouver l'expression l' expression de ta tangente
pour trouver l'expression l' expression de ta tangente
1+(x-y) +o(x-y) -(1+x+y) = 0 soit y=....
Tu as donc un vecteur directeur de ta tangente et tu vérifies que le gradient est bien orthogonal.
{à vérifier!!!}
Tu peux aussi utiliser
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
