Optimisation : géométrie synthétique

[srhmrc]

Bonjour, je n'arrive pas à résoudre cet exercice :
Une pyramide à base quadrangulaire de hauteur h est inscrite dans une sphère de rayon r. Détermine :
1) V(h)
2) h lorsque V(h) est maximal

[Ben314]

Si on ne suppose pas que la pyramide est régulière c'est à dire que les 4 faces triangulaires sont isométriques (ce qui implique que le pied du sommet est le milieu du carré, ) alors il y a des tonnes de solutions de volume différents pour une même hauteur h.
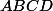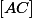Si on suppose la pyramide régulière de base le carré de coté et de sommet situé sur la perpendiculaire au plan de base passant par le centre du carré et tel que alors est le milieu de et on connait (en fonction de et ) les dimensions du triangle isocèle . De plus, on sait que ce triangle est inscrit dans un cercle de rayon ce qui permet d'avoir en fonction de et .