Opération sur les ensembles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Juin 2019, 21:28
par mehdi-128 » 06 Juin 2019, 21:28
-
azertytreza
- Membre Relatif
- Messages: 163
- Enregistré le: 26 Mai 2019, 15:51
-
 par azertytreza » 06 Juin 2019, 21:53
par azertytreza » 06 Juin 2019, 21:53
Bonjour
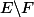
se nomme le complément de F dans E
cette opération est possible que uniquement si
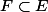
par contre
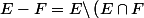)
cette opération est toujours possible
Dans l'anneau de Boole
l'opération
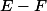
est l'opération
)
En ce qui concerne la différence symétrique
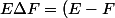\cup\left(F-E\right))
cette opération est toujours possible
dans l'anneau de Boole c'est l'opération
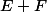
Modifié en dernier par
azertytreza le 07 Juin 2019, 00:26, modifié 3 fois.
-
noobey
- Membre Naturel
- Messages: 41
- Enregistré le: 17 Avr 2019, 15:51
-
 par noobey » 06 Juin 2019, 21:53
par noobey » 06 Juin 2019, 21:53
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Juin 2019, 23:25
par mehdi-128 » 06 Juin 2019, 23:25
Je l'ai posté ici car je n'ai toujours pas compris pourquoi on peut se passer de préciser

dans :
\Leftrightarrow x \notin A)
Alors que la définition donne :
\Leftrightarrow (x \in E \ ET \ x \notin A ))
On m'a répondu que

par hypothèse mais je n'ai pas compris pourquoi forcément

est dans

du coup l'implication :
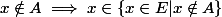
ne me paraît pas trivial

Pour

serait forcément dans

?
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 07 Juin 2019, 08:20
par beagle » 07 Juin 2019, 08:20
Si x n'appartient ni à A ni à E, je veux bien le prendre
pour chez moi, j'en ai plus.
mais si quelqu'un d'autre en a besoin…
PS: il était à qui x au départ?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Juin 2019, 08:47
par mehdi-128 » 07 Juin 2019, 08:47
Justement rien n'est dit sur x. On dit juste que A est un ensemble inclus dans E.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 07 Juin 2019, 08:49
par beagle » 07 Juin 2019, 08:49
mehdi-128 a écrit:Justement rien n'est dit sur x. On dit juste que A est un ensemble inclus dans E.
mais si on bosse dans E, x est est dans A ou dans le complémentaire.
Par contre si tu bosses dans F avec E inclus dans F, ben t'as raison, ça craint.
Donc faut voir ton énoncé.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 07 Juin 2019, 09:37
par chombier » 07 Juin 2019, 09:37
L'équivalence
\Longleftrightarrow x \notin A)
n'est vraie que si on suppose depuis le départ que x est un élément de E (On "travaille" dans E).
Il y a plusieurs façons de l'écrire :
1)
\Longleftrightarrow x \notin A)
2)
\Longleftrightarrow x \notin A))
3)
\Longleftrightarrow x \in E \text{ et } x \notin A))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Juin 2019, 09:51
par mehdi-128 » 07 Juin 2019, 09:51
Merci pour vos réponses très claires.
Du coup, si je veux démontrer que pour
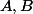
des parties de

:
 =\complement_E (A) \cup \complement_E (B))
Si j'écris :
 \Leftrightarrow x \notin A \cap B \Leftrightarrow x \notin A \cup x \notin B \Leftrightarrow x \in \complement_E(A) \cup x \in \complement_E(B))
C'est juste où je dois rajouter le

? Comment savoir à partir de l'énoncé si on raisonne que dans

?

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 07 Juin 2019, 09:56
par chombier » 07 Juin 2019, 09:56
Il faut l'écrire avant :
Soit x un élément (quelconque) de E. Alors :
 \Leftrightarrow x \notin A \cap B \Leftrightarrow x \notin A \lor x \notin B \Leftrightarrow x \in \complement_E(A) \lor x \in \complement_E(B) \Leftrightarrow x \in \complement_E(A) \cup \complement_E(B))
Modifié en dernier par
chombier le 07 Juin 2019, 10:17, modifié 4 fois.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Juin 2019, 10:08
par mehdi-128 » 07 Juin 2019, 10:08
D'accord merci !

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 07 Juin 2019, 10:14
par chombier » 07 Juin 2019, 10:14
Attention, le symbole "
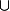
" ne signifie pas "et"
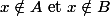
doit s'écrire :
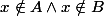
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Juin 2019, 10:30
par mehdi-128 » 07 Juin 2019, 10:30
Oui j'ai fait une erreur d'étourderie.
Je cherche à déterminer :
)
et
)
 = \{x \in E , x \notin E \})
 = \{x \in E , x \notin \emptyset \})
Mais comment simplifier ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités