Norme d'une matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 21:02
par izoard » 09 Fév 2012, 21:02
Bonjour,
que peut on dire de la norme de la transposée d'une matrice par rapport à la norme de la matrice elle même ??
Même question avec la norme de l'inverse d'une matrice ??
Merci
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 09 Fév 2012, 21:53
par Le_chat » 09 Fév 2012, 21:53
Salut. Il y a pas mal de normes sur les matrices, il va être difficile de s'entendre si tu ne dis pas de laquelle tu parles.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 21:54
par izoard » 09 Fév 2012, 21:54
Disons la norme subordonnée à la norme euclidienne
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 09 Fév 2012, 21:57
par girdav » 09 Fév 2012, 21:57
Dans ce cas c'est le rayon spectral de
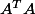
(si on travaille dans le cas réel) et comme on sait que si M et N sont deux matrices, MN et NM ont les même valeurs propres non nulles...
Par contre ce n'est pas vrai pour la norme subordonnée à la norme 1 ou la norme

.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 22:11
par izoard » 09 Fév 2012, 22:11
Si je comprends bien ,
d'après la propriété que tu cite
=\rho(A A^T))
Or
)
et
)
Donc
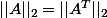
Par contre je ne vois pas comment demontrer cette fameuse propriété que l'on utilise ...
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 22:14
par izoard » 09 Fév 2012, 22:14
Ah non c'est simple en fait :we:
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 22:15
par izoard » 09 Fév 2012, 22:15
et au niveau de l'inverse, on peut dire quelque chose ??
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 09 Fév 2012, 22:19
par girdav » 09 Fév 2012, 22:19
Pour ce qui est de la norme subordonnée à la norme euclidienne, essaie de relier de rayon spectral de
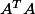
à celui de
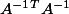
.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 22:30
par izoard » 09 Fév 2012, 22:30
^{-1}=A^{-1}(A^T)^{-1}=A^{-1}^TA^{-1})
Donc
^{-1})=\rho(A^{-1}^TA^{-1})=||A^{-1}||_2)
et comme
^{-1}))
n'est pas égal à
)
,
j'en déduit que
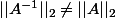
C'est ça ???
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 09 Fév 2012, 22:38
par girdav » 09 Fév 2012, 22:38
En fait en considérant
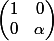
on voit qu'il n'y a pas de lien entre les deux quantités.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 09 Fév 2012, 22:46
par izoard » 09 Fév 2012, 22:46
OK . Merci beaucoup !!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
