Nombre complexe equation
16 messages
- Page 1 sur 1
Nombre complexe equation
bonsoir,
Voila j'ai une équation à résoudre et il faut trouver le module de chaque solution ainsi que son argument
z^2-2zsin x + 2(1+cos x) =0
Sachant (sin x)^2 - 2(1+cos x )= -4 (cos (x/2))^4
moi je trouve les solutions suivantes z= 2;)(1-(cos x)^2) + ou - 4i(cos (x/2))^2
ensuite je trouve lzl= 2;)(2(1+cos x))
et cos ;) =;)((1-(cos x)^2)/(1+cos x))
et sin ;) = (-4(cos (x/2))^2)/;)(2(1+cos x))
Je ne sais pas comment faire pour trouver l'argument, je n'arrive pas à simplifier les expressions
merci
Voila j'ai une équation à résoudre et il faut trouver le module de chaque solution ainsi que son argument
z^2-2zsin x + 2(1+cos x) =0
Sachant (sin x)^2 - 2(1+cos x )= -4 (cos (x/2))^4
moi je trouve les solutions suivantes z= 2;)(1-(cos x)^2) + ou - 4i(cos (x/2))^2
ensuite je trouve lzl= 2;)(2(1+cos x))
et cos ;) =;)((1-(cos x)^2)/(1+cos x))
et sin ;) = (-4(cos (x/2))^2)/;)(2(1+cos x))
Je ne sais pas comment faire pour trouver l'argument, je n'arrive pas à simplifier les expressions
merci
mathos92 a écrit:bonsoir,
Voila j'ai une équation à résoudre et il faut trouver le module de chaque solution ainsi que son argument
z^2-2zsin x + 2(1+cos x) =0
Sachant (sin x)^2 - 2(1+cos x )= -4 (cos (x/2))^4
moi je trouve les solutions suivantes z= 2;)(1-(cos x)^2) + ou - 4i(cos (x/2))^2
ensuite je trouve lzl= 2;)(2(1+cos x))
et cos=;)((1-(cos x)^2)/(1+cos x))
et sin= (-4(cos (x/2))^2)/;)(2(1+cos x))
Je ne sais pas comment faire pour trouver l'argument, je n'arrive pas à simplifier les expressions
merci
slt
transforme d'abord le module
tu dois avoir 2|cos(x/2)|
Salut,
Je comprend pas trop d'où tu sort la racine carrée dans 2;)(1-(cos x)^2).
La formule, c'est pas où
où 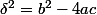 ?
?
Pourquoi n'a tu pas gardé le sin(x) de départ ?
Après, ce sin(x), comme tout le reste, il faut l'exprimer en fonction de l'angle moitié x/2.
mathos92 a écrit:... z= 2;)(1-(cos x)^2) + ou - 4i(cos (x/2))^2
Je comprend pas trop d'où tu sort la racine carrée dans 2;)(1-(cos x)^2).
La formule, c'est pas
Pourquoi n'a tu pas gardé le sin(x) de départ ?
Après, ce sin(x), comme tout le reste, il faut l'exprimer en fonction de l'angle moitié x/2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'ai mis tous selon cos car il le demande dans une question
Voici le détail de mon calcul:
z^2 - 2zsin x + 2(1+cos x)=0
delta= -16(cos (x/2))^4
Z= 2sinx -i;)(16(cos (x/2))^4) = 2;)(1-(cos x)^2) + 4i(cos (x/2))^2
lzl= ;)(2;)(1-(cos x)^2) + (-4(cos(x/2)^2))
= ;)(4(1-(cos x)^2)+16(cos (x/2)^4))
= 2;)(1- (cos x)^2 +4 (cos(x/2)^4))
=2;)(1-(cos x)^2 - (sin x)^2 +2 + 2cosx)
= 2;)2(1+cos x))
et même là j'arrive pas à trouver comme chan79
comment je peut modifier ce résultat pour trouver 2cos(x/2) ?
Merci
Voici le détail de mon calcul:
z^2 - 2zsin x + 2(1+cos x)=0
delta= -16(cos (x/2))^4
Z= 2sinx -i;)(16(cos (x/2))^4) = 2;)(1-(cos x)^2) + 4i(cos (x/2))^2
lzl= ;)(2;)(1-(cos x)^2) + (-4(cos(x/2)^2))
= ;)(4(1-(cos x)^2)+16(cos (x/2)^4))
= 2;)(1- (cos x)^2 +4 (cos(x/2)^4))
=2;)(1-(cos x)^2 - (sin x)^2 +2 + 2cosx)
= 2;)2(1+cos x))
et même là j'arrive pas à trouver comme chan79
comment je peut modifier ce résultat pour trouver 2cos(x/2) ?
Merci
mathos92 a écrit:J'ai mis tous selon cos car il le demande dans une question
Voici le détail de mon calcul:
z^2 - 2zsin x + 2(1+cos x)=0
delta= -16(cos (x/2))^4
Z= 2sinx -i;)(16(cos (x/2))^4) = 2;)(1-(cos x)^2) + 4i(cos (x/2))^2
lzl=(2;)(1-(cos x)^2) + (-4(cos(x/2)^2))
=(4(1-(cos x)^2)+16(cos (x/2)^4))
= 2;)(1- (cos x)^2 +4 (cos(x/2)^4))
=2;)(1-(cos x)^2 - (sin x)^2 +2 + 2cosx)
= 2;)2(1+cos x))
et même là j'arrive pas à trouver comme chan79
comment je peut modifier ce résultat pour trouver 2cos(x/2) ?
Merci
le discriminant réduit de l'équation initiale est
les solutions sont
module=
C'est un "vieux truc" (j'espère que chan ne m'en voudra pas...)
Au lieu de faire
 puis
puis 
Lorsque b se divise facilement par 2, tu pose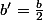 et tu fait
et tu fait
 puis
puis 
ça ne change évidement rien et ça va plus vite (on appelle ça le discriminant "réduit").
Au lieu de faire
Lorsque b se divise facilement par 2, tu pose
ça ne change évidement rien et ça va plus vite (on appelle ça le discriminant "réduit").
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tu t'est trompé quelque part (en particulier, comme Z1 et Z2 sont conjugués, leurs argument sont les même au signe prés donc les cosinus sont les mêmes et les sinus sont opposés.
En reprenant ce que chang a fait :
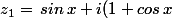) et
et 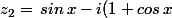)
 où
où 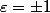 selon que
selon que  ou pas.
ou pas.
Bon, déjà, si alors
alors  n'ont pas d'argument bien définis.
n'ont pas d'argument bien définis.
Sinon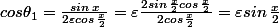
et}{2 cos\,\frac{x}{2}}=\varepsilon cos\,\frac{x}{2})
Si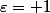 , l'angle
, l'angle 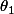 de cosinus
de cosinus  et de sinus
et de sinus  est
est  (fait un dessin)
(fait un dessin)
Si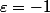 , l'angle
, l'angle 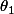 de cosinus
de cosinus  et de sinus
et de sinus  est ... (refait un dessin)
est ... (refait un dessin)
Et pour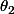 , il n'y a rien à recalculer
, il n'y a rien à recalculer  vu que
vu que 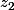 est le conjugué de
est le conjugué de 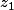
En reprenant ce que chang a fait :
Bon, déjà, si
Sinon
et
Si
Si
Et pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
