Nature de la série avec une partie entière

[ERRAZKA]

Bonjour tout le monde.
On chercher à déterminer la nature de la série de terme général .
Merci d'avance.

[Ben314]

Salut,
Pour un entier donné, ça donne quoi la somme des termes tels que ?
Conclusion.

[ERRAZKA]

Bonjour,
à p donné, la somme des termes sur vaut , car on somme sur un ensemble fini de cardinal . Même la série de terme général est une série alternée convergente, on ne peut pas conclure la convergence de la série, car il s'agit d'appliquer le théorème de sommation par paquets mais les termes ne sont pas positifs pour le faire !
Merci de vérifier ce point.

[Ben314]

Je ne sait pas trop ce que c'est que tu appelle "le théorème de sommation par paquets", mais là, ce que je vois, c'est que la série des est convergente et que les sommes partielles de la séries de départ sont systématiquement comprises entre deux somme partielles successives de cette nouvelle série.

[capitaine nuggets]

Salut !

Bonjour,
à p donné, la somme des termes sur vaut , car on somme sur un ensemble fini de cardinal . Même la série de terme général est une série alternée convergente, on ne peut pas conclure la convergence de la série, car il s'agit d'appliquer le théorème de sommation par paquets mais les termes ne sont pas positifs pour le faire !
Merci de vérifier ce point.

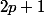
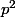
Petite erreur : il y a entiers tels que : ce sont tous les entiers compris entre et .