Multiplicateur de Lagrange

[super_teufel]

Salut tlm,

Je doit optimiser avec la contrainte g(x,y)=(xy)-8=0 ,

J'obtiens les points (4,2) (-4,-2)

Je désire savoir comment faire pour évaluer si c'est max ou un min. Mes notes de cours disent qu'il faut évaluer f(a,b) , mais (4,2) ; (-4,-2) donne la même chose.

(-4,-2) est sensé être un max
(4,2) l'inverse

Merci de m'éclaicir.

[busard_des_roseaux]

bjr,

Ton résultat semble erroné.
La variété est une hyperbole d'équation:

Cette équation en est une paramétrisation locale.
la fonction de R dans R:
doit avoir un extremum
donc un nombre dérivé nul,
soit

d'où (x,y)=(8;1)
f ''(8) > 0. Il s'agit d'un minimum.

Sauf erreur.

[super_teufel]

Ouais désolé, j'ai oublié de mettre le x à la 2. Je l'avais modifier ,mais ça pas marcher.

Effectivement, le point (1,8) est plus gros que (4,2)

[busard_des_roseaux]

Ouais désolé, j'ai oublié de mettre le x à la 2. Je l'avais modifier ,mais ça pas marcher.

Quel est l'énoncé exact ?

[super_teufel]

Je l'ai changer. En fait, je croit que les 2 point sont des minimum non?

Il y a quelque chose qui semble ne pas marcher

(4,2)(-4,-2) semble être des points minimum

et (0,infini ) ou (0,-infini) des points maximal

[busard_des_roseaux]

Soient ou
car
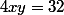
Il s'agit donc de minima absolus.