Ok j'ai regardé :we:
Je pense avoir compris ce qu'est la notion de miroir d'un mot. En fait si un mot s'écrit bbcdf alors le miroir de ce mot est fdcbb
L'équivalence qu'il faut démontrer consiste juste à dire que l'on peut indifféremment "inverser" un mot par la gauche ou par la droite.
Je ne comprend pas trop le
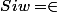
(en fait, je comprend que si le mot a une lettre alors son miroir est lui même)
Faisons un démonstration par récurrence la longueur n d'un mot.
- Le cas où le mot est de longueur 1 est évident.
- Hypothèse de récurrence : (HR) il existe un entier k supérieur ou égal à 1 tel que les deux définition sont équivalentes lorsque |w|=k.
- Soit M un mot de longueur k+1. Montrons que les deux définitions sont équivalentes.
On part de la première définition :
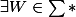
tel que
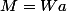
et
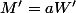
(1)
on va montrer que dans ce cas
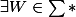
tel que
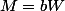
et
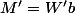
il n'y aucune raison pour que ce
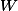
soit le même que celui du dessus. Mais l'écriture
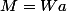
implique que
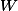
est de longueur k, donc il existe un mot

tel que
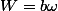
et donc :
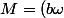a=b(\omega a))
(on se retrouve bien avec une écriture du type
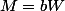
).
Gardons ces notations :
Donc :
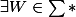
tel que
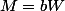
(avec
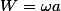
)
Oui mais alors,
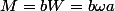
D'après (1) on conclut que :
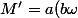')
D'après (HR) comme
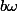
est de longueur k, on peut écrire :
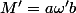
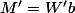
(on reconnaît
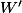
grâce à (HR))
Il me semble que l'on a écrit que des équivalences ici, et donc voilà la propriété démontrer au rang k+1.
On conclut que les définition sont équivalentes quelle que soit la longueur n du mot.



