Montrer une somme directe

[PCTroyes]

Bonsoir,
Voici le problème : K un espace vectoriel.
Phi une forme linéaire NON nulle de E
H= Ker (Phi) et x un vecteur de E qui n'appartient pas à H.

- Mq E= H (+) Vect(x)
(+) == somme directe.

J'ai dis que Phi étant une forme linéaire non nulle == Ker(phi) est un hyperplan de E
Donc dim(E) = dim(H) +1
Or dim(x) = 1 car c'est un vecteur donc dim(E) = dim(H) + dim(x)

Pour l'intersection je voulais utiliser Grassman.

PROBLEME: E n'est pas supposé fini non on ne peut même pas écrire dim(H).
De plus le "== Ker(phi) est un hyperplan de E" je ne suis pas censé le savoir donc pas censé l'utiliser...

Quelqu'un peut m'aider ?

[Pseuda]

Montrer que :

1) H ;) Vect (x) = {0}
2) H + Vect (x) = E

[zygomatique]

salut

f est une forme linéaire non nulle donc il existe un vecteur u tel que f(u) <> 0

et alors on en déduit que Im(f) = R

le théorème du rang permet de conclure que Dim Ker (f) + 1 = Dim E

donc Ker f est un hyperplan H

x n'appartient pas à H donc E = H +

soit e un élément de E ... il existe donc un scalaire p tels que e = h + kx où h est un élément de H

supposons qu'il n'y ait pas unicité donc ....


EDIT : supprimer un scalaire inutile

[Robot]

zygomatique, tu utilises aussi la dimension.

Il suffit de montrer que pour tout il existe et tels que , et qu'un tel couple est unique.
On peut raisonner par analyse-synthèse. Indication : si comme ci-dessus, alors

[zygomatique]

oui effectivement ...

ne garder que mes deux dernières lignes ....

[PCTroyes]

Merci pour vos réponses...
Je comprend qu'il faut que j'utilise le fait qu'une somme est directe si cette somme est unique. Et je vous remercie pour cela mais comment le montrer ?
L'analyse-synthèse me fait bloquer à Phi(v)+Lambda*Phi(x)...
Je ne vois pas en quoi partir de Phi(u) me montrera que la somme est directe.
Puis par dessus ça mon prof me dit de revenir à la définition d'un sev supplémentaire mais je pense qu'il s'est trompé de question alors comme ça !!!

Encore merci mais je n'ai pas tellement avancé je fais du sur place. Si seulement cette dimension était finie ça serait torché !!!

[zygomatique]

u = h + ax
u = h' + bx

f(u) = af(x)
f(u) = bf(x)

donc af(x) = bf(x)

or f(x) <> 0 donc .....

[PCTroyes]

u = h + ax
u = h' + bx

f(u) = af(x)
f(u) = bf(x)

donc af(x) = bf(x)

or f(x) 0 donc .....

il y a unicité car a=b...
M E R C I

[zygomatique]

il faut ensuite montrer que h = h' !!!!

[PCTroyes]

il faut ensuite montrer que h = h' !!!!

Ce n'est pas évident si on dit que h appartient au noyau de Phi : la forme linéaire non nulle ?
Vue que l'on a Phi(h)=Phi(h')=0 ?

[zygomatique]

un peu de sérieux on en est à ::

u = h + ax
u = h' + ax

comment conclure ?

[PCTroyes]

un peu de sérieux on en est à ::

u = h + ax
u = h' + ax

comment conclure ?

Au temps pour moi...
On isole h puis h'.
Désolé.
Encore merci

[zygomatique]

on soustrait tout simplement ...

de rien

[Robot]

Montrer l'unicité se fait directement par l'analyse. Inutile de le refaire !

Tu n'as pas mordu à mon hameçon, qui était pourtant gros ! Dommage ...

... si comme ci-dessus, alors

alors car . Donc , et .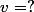
Inutile de montrer une nouvelle fois l'unicité, l'analyse la donne gratos !
Après dans la partie synthèse il ne reste plus qu'à vérifier que les valeurs trouvées pour et satisfont bien aux conditions voulues.

Ton prof avait bien raison, il fallait revenir à la définition de somme directe, à savoir existence et unicité de la décomposition suivant les deux sous-espaces. La partie analyse du raisonnement consistait à supposer l'existence d'une décomposition pour en déduire ce que valent nécessairement les deux morceaux de la décomposition. La partie synthèse est la vérification que les valeurs trouvées marchent bien.
Ce type de raisonnement est assez habituel pour établir des sommes directes : par exemple, pour établir que l'espace de toutes les fonctions de dans est la somme directe du sous-espace des fonctions paires et du sous-espace des fonctions impaires.

[zygomatique]

oui effectivement ... mais bon ...

merci Robot ...