Bonjour,
(j'ai une licence math) Dans une correction d'exercice j'ai :
1/2 (exp(x) -exp(-x)) >= 1/4 exp(x)
c'est certainement evident! mais je n'arive pas le montrer clairement... :mur:
si quelqu'un peu m'aider... :we:
Merci
Minorer une exponetielle..
10 messages
- Page 1 sur 1
J'ai pas vraiment le temps de me pencher en détail sur le problème mais j'ai juste une petite idée comme ça :
Ne pourrait-on pas considérer la fonction = \frac{\exp (x) - \exp (-x)}{2} - \frac{\exp (x)}{4}) qui correspond à ton problème ?
qui correspond à ton problème ?
On dérive et on prouve qu'elle est strictement croissante sur IR.
Ensuite, on dit que = -\infty)
Et que : = +\infty)
Et après on a plus qu'a chercher f(x) = 0 pour trouver pour quelles valeurs de x :1/2 (exp(x) -exp(-x)) >= 1/4 exp(x)
ça marche comme ça ?
Ne pourrait-on pas considérer la fonction
On dérive et on prouve qu'elle est strictement croissante sur IR.
Ensuite, on dit que
Et que :
Et après on a plus qu'a chercher f(x) = 0 pour trouver pour quelles valeurs de x :1/2 (exp(x) -exp(-x)) >= 1/4 exp(x)
ça marche comme ça ?
En fait c'étais pour calculer une majoration du module de ch(x) utile dans le calcul d'une integrale suivant un contour particulier.......et on prend x tend vers l'infini (pour retrouver l'intégrale demandé) le resultat devient alors evident!
:marteau: (il manquait bien une hypothése):marteau:
merci :happy3:
:marteau: (il manquait bien une hypothése):marteau:
merci :happy3:
bjr,
autre méthode, en posant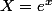 , on se ramène à l'étude du signe du trinôme.
, on se ramène à l'étude du signe du trinôme.
évidemment, pour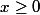
 \geq \frac{e^x}{2} \geq sh(x))
PS: passé d'excellentes vacances à la campagne:
1) chaque moucheron d'un nuage d'insectes semble suivre une trajectoire brownienne
2) Les gouttes de pluie, sur la surface des lacs, dessinent des stalagmites,
comme des champs de vecteurs aléatoires. Il semble que l'ensemble est discret et qu'il existe une distance minimale entre deux gouttes d'eau,
sur le plan du lac.
autre méthode, en posant
évidemment, pour
PS: passé d'excellentes vacances à la campagne:
1) chaque moucheron d'un nuage d'insectes semble suivre une trajectoire brownienne
2) Les gouttes de pluie, sur la surface des lacs, dessinent des stalagmites,
comme des champs de vecteurs aléatoires. Il semble que l'ensemble est discret et qu'il existe une distance minimale entre deux gouttes d'eau,
sur le plan du lac.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
