Mini question

[simplet]

Bonjour,
une fpnction constante n'est pas intégrable par rapport à la mesure de Lebesgue. Quand n'est-il au sens de Riemann?? c'est toujours le cas?
mercii
(l'objet ne ment pas :-)

[Touriste]

Bonjour,

C'est pareil pour Riemann et Lebesgue. Bien sûr les fonctions constantes sont intégrables dans les deux cas si tu les considères sur des compacts ou du moins sur des ensembles de mesure de Lebesgue finie.

[quinto]

Ca dépend de ce que tu entends pas intégrable.
En général on dit qu'une fonction f est intégrable si
est fini.
Sauf erreur.

[simplet]

oui oui excusez moi,
j'ai oublié de dire que je considérais R l'ensemble des nombres reels comme domaine d'intégration: une fonction constante n'est pas intégrable sur R par rapport à la mesure de Lebesgue (ca ok)
mais je pensais qu'elle était Riemann intégrable (la def de Riemann intégrable ne contradit rien ici..si?)
merci

[abcd22]

Bonjour,

la def de Riemann intégrable ne contradit rien ici..si?

Euh, si, une fonction f est Riemann-intégrable sur un intervalle I si , où K est un segment (c'est comme ça qu'on a défini les fonctions intégrables en sup en tout cas), ce n'est pas le cas avec f constante et 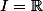... C'est étonnant que tu te poses la question pour Riemann après te l'être posée pour Lebesgue, d'habitude on voit l'intégrale de Riemann d'abord. :happy2:

[serge75]

Une fonction ne saurait être Riemann intégrable sur R, vu que l'intégrale de Riemann ne concerne que l'intégrale sur un segment.
En tant qu'intégrale généralisée, ça ne marche pas non plus : elle est clairement divergente.

Enfin, un autre point de vue : toute fonction intégrable au sens de Riemann l'est au sens de Lebesgue. Ta fonction n'étant pas Lebesgue-intégrable, elle l'est encore moins au sens de Riemann.
Cordialement