Bonjour,
(Condition initial)
N(0)=1
N'=-2tN
1-En appliquant la méthode Euler, avec le taux d'accroissement [N(t+h)-N(t)]/h au lieu de N' et avec un pas h=0,25,
déterminer N(t) de proche en proche jusqu'a N(2)
Je ne sais pas du tout faire ca je sais juste que
[N(t+h)-N(t)]/h=KN(t)
Or il n'y pas de constante K...
2-En isolant N'/N (N'/N=k), résoudre l'équation différentielle en écrivant N(t) de maniéré explicite
Je comprend pas non plus :(
Métohde euler - taux d'acroissement eq diff
6 messages
- Page 1 sur 1
kadic25 a écrit:Bonjour,
(Condition initial)
N(0)=1
N'=-2tN
1-En appliquant la méthode Euler, avec le taux d'accroissement [N(t+h)-N(t)]/h au lieu de N' et avec un pas h=0,25,
déterminer N(t) de proche en proche jusqu'a N(2)
Je ne sais pas du tout faire ca je sais juste que
[N(t+h)-N(t)]/h=KN(t)
Or il n'y pas de constante K...
Bah, tu écris [N(0,25) - N(0)]/0,25 = -2x0xN(0) et tu obtiens la valeur de N(0,25) facilement
et tu recommences [N(0,5)-N(0,25)]/0,25 = -2x0,25xN(0,25) et tu obtiens la valeur de N(0,5)...
A ta place, à moins que ça ne soit clairement spécifié de tout faire à la main, je ferais ça avec un tableur, ce qui en particulier me permettrais en 10 secondes de plus de regarder ce qu'il se passe si on prend un pas plus petit puis, une fois l'équation théorique résolue, de regarder si ça donne de bon résultat ou pas.
Perso, le tableur me donne N(2)=0,00240325927734375 si je prend un pas de 0,25 (et N(2)=0,0120230515952439 avec un pas de 0,1) alors que la valeur exacte est de N(2)=0,0183156388887342
Perso, le tableur me donne N(2)=0,00240325927734375 si je prend un pas de 0,25 (et N(2)=0,0120230515952439 avec un pas de 0,1) alors que la valeur exacte est de N(2)=0,0183156388887342
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:A ta place, à moins que ça ne soit clairement spécifié de tout faire à la main, je ferais ça avec un tableur, ce qui en particulier me permettrais en 10 secondes de plus de regarder ce qu'il se passe si on prend un pas plus petit puis, une fois l'équation théorique résolue, de regarder si ça donne de bon résultat ou pas.
Perso, le tableur me donne N(2)=0,00240325927734375 si je prend un pas de 0,25 (et N(2)=0,0120230515952439 avec un pas de 0,1) alors que la valeur exacte est de N(2)=0,0183156388887342
Bsr,
Question idiote : que met tu dans les cases du tableur?
Une ligne pour t, une ligne pour N'(t), et une ligne pour N(t).
Et évidement une cas "à part" pour le pas h histoire de pouvoir le modifier.
Et il te suffit de transcrire mot à mot le fait que :
1)
2)=-2tN(t_i))
3)=N(t_i)+h.N'(t_i))
Et évidement les "conditions initiales"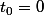 et
et =1)
Et évidement une cas "à part" pour le pas h histoire de pouvoir le modifier.
Et il te suffit de transcrire mot à mot le fait que :
1)
2)
3)
Et évidement les "conditions initiales"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
