Méthode des trapèzes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
par AceVentura » 13 Mar 2010, 23:42
Bonsoir. Désignant par
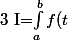dt)
et par
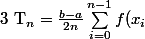+f(x_{i+1}))
, je dois démontrer que
^3}{12n^2})
.
NB : notations classique
,
et
|)
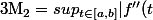Indication : utiliser la fonction
=\frac{f(x_i)+f(x_i+h)}{2}h-\int_{x_i}^{x_i+h}f(t)dt)
.
J'ai fait les dessins, et je crois avoir compris le truc. Mais j'ai des soucis de notations.
D'une part :
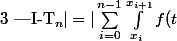dt-\frac{b-a}{2n}\sum_{i=0}^{n-1}f(x_i)+f(x_{i+1})|\le \sum_{i=0}^{n-1}|\Delta(h)|)
.
D'autre part :
=0)
=\frac{1}{2}(f\prime(x_i+h)h+f(x_i)+f(x_i+h))-f(x_i+h)=\frac{1}{2}(f\prime(x_i+h)h+f(x_i)-f(x_i+h)))
donc
=0)
}(h)=\frac{1}{2}(f ^{(2)}(x_i+h)h+f\prime(x_i+h)-f\prime(x_i+h))=\frac{f ^{(2)}(x_i+h)h}{2})
donc
}(0)=0)
}(h)=\frac{1}{2}(f^{(3)}(x_i+h)h+f^{(2)}(x_i+h)))
En utilisant l'inégalité de Taylor-Lagrange sur le segment [0,h], je trouve :
|=|\Delta(h)-\sum_{k=0}^{2}\frac{\Delta^{(k)}(0)}{k!}h^k|\le \sup_h |\Delta^{(3)}(h)|\times\frac{h^3}{3!})
.
Puis
}(h)| \times \frac{h^3}{3!} = \sup_{h} |\frac{1}{2}(f^{(3)}(x_i+h)h+f^{(2)}(x_i+h))| \times \frac{(b-a)^3}{6n^3} =\sup_{h} |f^{(3)}(x_i+h)h+f^{(2)}(x_i+h)| \times \frac{(b-a)^3}{12n^3})
Je n'arrive pas à me convaincre que
}(x_i+h)h+f^{(2)}(x_i+h)| \le sup_{t\in [a,b]}|f ^{(2)}(t)|)
ce qui donnerait immédiatement le résultat par sommation.
Merci par avance !
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
par lapras » 14 Mar 2010, 19:12
salut,
en fait il faut faire une intégration par partie de f et faire apparaitre la constante (f(a)+f(b))/2*h dans les termes "entre crochet".
On obtiendra : int(a,b) f(t).dt = (f(a)+f(b))/2*(b-a) + int(a,b) (f''(t)*(t-a)(t-b)/2dt)
D'où le résultat en majorant f''(t) par son sup.
PS : il ne faut pas utiliser de f^(3) car f n'est a priori par C3.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
