Bonjour,je suis nouveau sur ce forum.
Je me souviens avoir fait il y a longtemps,en prépa,un exercice qui exhibait une matrice A (3,3),ayant une propriété particulière.
En effet si x^2+y^2=z^2,alors si A*(x,y,z)=(X,Y,Z),on a X^2+Y^2=Z^2.
Désolé,je ne sais pas comment mettre les exposants(x^2 désignera le carré de x).J'aimerais retrouver cette matrice.
On m'a parlé de matrices orthogonales,mais je ne vois toujours pas pourquoi.
Je serais curieux de retrouver cette matrice et de pouvoir en engendrer d'autres.
D'autre part,un de mes profs m'a dit qu'on connaissait tous les triplets de nombres vérifiant cette "propriété de Fermat",comme le fameux (3,4,5).
Peut-on me dire comment les obtenir tous?
Merci d'avance!
Matrices "de Fermat"
3 messages
- Page 1 sur 1
Triplets de Fermat
On sait effectivement trouver tous les triplets (a, b, c) vérifiant 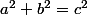 :
:
Soit donc un tel triplet. Il est clair que tout facteur premier divisant deux des termes divise aussi le troisième, on peut donc supposer que a, b et c sont deux à deux premiers entre eux.
Ensuite, des congruences modulo 4 montrent que un des deux nombres a ou b est pair, l'autre impair et que c est impair. En effet, les carrés des nombres pairs sont congrus à 0 modulo 4, et ceux des nombres impairs à 1 modulo 4.
Supposons donc a pair, a = 2a'. On a donc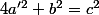 soit
soit 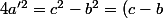(c+b)) . c-b et c+b sont tous deux pairs, Après simplification par 2, on a
. c-b et c+b sont tous deux pairs, Après simplification par 2, on a 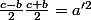 , et
, et  et
et  n'ont pas de facteur premier impair (sinon ce gfacteur diviserait leur somme c et leur diférence b, et on a supposé que b et c sont premiers entre eux. Comme les entiers premiers entre eux
n'ont pas de facteur premier impair (sinon ce gfacteur diviserait leur somme c et leur diférence b, et on a supposé que b et c sont premiers entre eux. Comme les entiers premiers entre eux  et
et  ont pour produit un carré, ce sont tous deux des carrés. On a donc
ont pour produit un carré, ce sont tous deux des carrés. On a donc 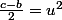 et
et 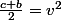 , soit par somme et différence
, soit par somme et différence 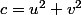 et
et 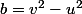 , et comme
, et comme 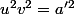 , on a
, on a 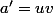 et
et 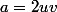 . Les solutions sont donc
. Les solutions sont donc
^2+(v^2-u^2)^2=(u^2+v^2)^2)
Pour que nos trois entiers spoient premiers entre eux, il faut que u et v soient premiers entre eux, et de parités différentes.
Remarque : cette démonstration figure dans le livre "L'arithmétique" de Diophante, dont la traduction par Bachet était possédée par Pierre Fermat. C'est en marge de cette solution que Fermat à écrit la phrase célèbre "Par contre, la somme de deux cubes ne peut jamais être un cube, la somme de deux puissances quatrièmes une puissance quatrième, ni en général la somme de deux puissances une puissance de même niveau. J'ai découvert une démonstration merveilleuse de ce résultat, malheureusement je n'ai pas la place de l'écrire dans cette marge"
Soit donc un tel triplet. Il est clair que tout facteur premier divisant deux des termes divise aussi le troisième, on peut donc supposer que a, b et c sont deux à deux premiers entre eux.
Ensuite, des congruences modulo 4 montrent que un des deux nombres a ou b est pair, l'autre impair et que c est impair. En effet, les carrés des nombres pairs sont congrus à 0 modulo 4, et ceux des nombres impairs à 1 modulo 4.
Supposons donc a pair, a = 2a'. On a donc
Pour que nos trois entiers spoient premiers entre eux, il faut que u et v soient premiers entre eux, et de parités différentes.
Remarque : cette démonstration figure dans le livre "L'arithmétique" de Diophante, dont la traduction par Bachet était possédée par Pierre Fermat. C'est en marge de cette solution que Fermat à écrit la phrase célèbre "Par contre, la somme de deux cubes ne peut jamais être un cube, la somme de deux puissances quatrièmes une puissance quatrième, ni en général la somme de deux puissances une puissance de même niveau. J'ai découvert une démonstration merveilleuse de ce résultat, malheureusement je n'ai pas la place de l'écrire dans cette marge"
Matrices
Merci Galt,mais comment faîtes-vous pour trouver des matrices changeant un triplet de Fermat en un triplet de Fermat?
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
