Matrice, récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 11 Mar 2009, 21:29
par juju78 » 11 Mar 2009, 21:29
Bonjour
On note I3 la matrice idendité et 03 la matrice nulle de taille 3. par ailleurs on note

les coefficients binomiaux.
On considere
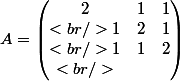
Determiner la matrice J telle que A= I3 + J
je trouve
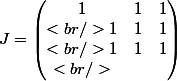
On me demande alors de calculer J²
je trouve
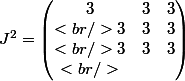
On me demande ensuite d'en déduire, pour tout n dans N*,

en fonction de J et n
On remarque que l'on a


Mais je ne vois pas comment établir une relation?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Mar 2009, 21:33
par Nightmare » 11 Mar 2009, 21:33
Bah tes nombres sont les puissances successives de 3 non?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Mar 2009, 21:41
par nuage » 11 Mar 2009, 21:41
Salut,
ton premier calcul donne

On a donc
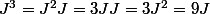
etc...
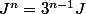
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 12 Mar 2009, 20:09
par juju78 » 12 Mar 2009, 20:09
a oui effectivement , merci
On a ensuite :
Montrer qu'on peut trouver deux réels x et y tels que
A² - xA + yI3 = 03
mais là c'est pareil je vois pas par ou commencer?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 13 Mar 2009, 08:43
par nuage » 13 Mar 2009, 08:43
Une méthode possible :
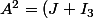^2)
on développe le produit et on remplace
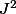
par

on reporte le tout dans la relation demandée
la suite est facile
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 12:21
par juju78 » 14 Mar 2009, 12:21
pour calculer A² on ne peut pas faire :
 \times (I3+J))
?
Au lieu de faire I² + 2JI + J² ?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 14 Mar 2009, 12:29
par nuage » 14 Mar 2009, 12:29
C'est la même chose.
Au passage JI=J
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 12:29
par juju78 » 14 Mar 2009, 12:29

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 14 Mar 2009, 12:41
par nuage » 14 Mar 2009, 12:41
Bien sur.
Disons que la méthode que je te propose permet de trouver x et y sans faire trop de calculs. Et en particulier sans effectuer de produit de matrices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
