Matrice de Kronecker ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 24 Fév 2010, 11:28
par MacErmite » 24 Fév 2010, 11:28
Bonjour,
Je ne comprends pas cette définition "Soit la notation

la matrice carré dont tout les coefficients sont nuls, sauf le coefficient (i,j) qui vaut 1"
J'ai compris que i désigne les lignes et j les colonnes, mais j'ai du mal à me représenté E, pouvez-vous m'aider ?
Cette notation est tout aussi nébuleuse : :briques:
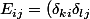_{kl})
,

si k=i

sinon :ptdr:
Merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 24 Fév 2010, 11:50
par Nightmare » 24 Fév 2010, 11:50
Salut,
Tout est dit, tous les coefs sont nuls sauf celui à la place (i,j) qui vaut 1.
Par exemple la matrice

est la matrice avec des 0 partout, sauf à la première ligne deuxième colonne ou elle a un 1.
Il est évident que les matrices Eij forment une base de l'ensemble des matrices/

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Fév 2010, 11:52
par Ben314 » 24 Fév 2010, 11:52
Exemple, si n=4 on a :
)
,
)
,
)
... etc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 24 Fév 2010, 11:57
par MacErmite » 24 Fév 2010, 11:57
Merci pour les exemples, c'est plus "parlant" pour moi.
Comment traduire cette notation :
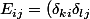_{kl})
,

si k=i

sinon
je ne comprends pas k,l...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Fév 2010, 12:04
par Ben314 » 24 Fév 2010, 12:04
C'est la façon "un peu pédante" (mais souvent utile) d'écrire exactement la même chose :
Pour i et j fixés,

est le produit de deux nombres qui valent soit 0, soit 1. Donc pour que le produit soit égal à 1 il faut (et il suffit) que les deux termes soit égaux à 1, c'est à dire que k=i et l=j. Evidement, dans tout les autres cas, le produit vaut 0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités