Je me suis récemment inscrit (il y a quelques minutes), et je bûche sur un exercice de maths financières depuis presque 4 heures ( je suis rouillé et je n'ai surement pas la bonne logique, j'ai l'impression que tous mes résultats sont faux).
Voici le problème :
"Monsieur Jean désire préparer sa retraite. Agé aujourd’hui de 35 ans, il souhaite effectuer
dès à présent des versements mensuels constants pour disposer à partir de 65 ans (âge de sa
retraite) d’une rente mensuelle de 2 500 €, pendant 18 ans (qui débute un mois après le
dernier versement par Monsieur Jean). Une compagnie d’assurance lui assure un taux
d’intérêt de 6%.
Quel est le montant des versements mensuels constants que doit effectuer Monsieur Jean."
Je constate donc qu'il lui faut 540 000€ sur 30 ans pour pouvoir bénéficier de sa rente mensuelle de 2500€.
Néanmoins, je n'arrive pas à déterminer quelle formule utiliser entre la valeur acquise, l'actualisation, etc. afin de résoudre le problème... Je sèche totalement...
J'ai beau tourner et retourner le problème, calculer et recalculer tout m'a l'air faux...
Merci d'avance pour votre aide ! et veuillez m'excuser si le problème et simple, mais je n'arrive pas à voir comment le résoudre "proprement" si je puis dire.Je me suis récemment inscrit (il y a quelques minutes), et je bûche sur un exercice de maths financières depuis presque 4 heures ( je suis rouillé et je n'ai surement pas la bonne logique, j'ai l'impression que tous mes résultats sont faux).
Voici le problème :
"Monsieur Jean désire préparer sa retraite. Agé aujourd’hui de 35 ans, il souhaite effectuer
dès à présent des versements mensuels constants pour disposer à partir de 65 ans (âge de sa
retraite) d’une rente mensuelle de 2 500 €, pendant 18 ans (qui débute un mois après le
dernier versement par Monsieur Jean). Une compagnie d’assurance lui assure un taux
d’intérêt de 6%.
Quel est le montant des versements mensuels constants que doit effectuer Monsieur Jean."
Je constate donc qu'il lui faut 540 000€ sur 30 ans pour pouvoir bénéficier de sa rente mensuelle de 2500€.
Néanmoins, je n'arrive pas à déterminer quelle formule utiliser entre la valeur acquise, l'actualisation, etc. afin de résoudre le problème... Je sèche totalement...
J'ai beau tourner et retourner le problème, calculer et recalculer tout m'a l'air faux...
Merci d'avance pour votre aide ! et veuillez m'excuser si le problème et simple, mais je n'arrive pas à voir comment le résoudre "proprement" si je puis dire.
Maths financières : suites géométriques, annuités
7 messages
- Page 1 sur 1
Re: Maths financières : suites géométriques, annuités
Bonjour, déjà posté ailleurs https://les-mathematiques.net/vanilla/index.php?p=/discussion/2329837/calcul-de-rentes
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Maths financières : suites géométriques, annuités
Je suis d'accord, néanmoins, cela ne m'aide pas vraiment puisqu'il n'y a pas d'explication.
J'ai cherché sur ces deux forums des réponses à mon sujet sans y trouver de réponse, d'où mes posts.
Comme la rubrique l'indique, nous sommes censés "nous entraider" non ?
Merci pour ton indulgence @kekia
J'ai cherché sur ces deux forums des réponses à mon sujet sans y trouver de réponse, d'où mes posts.
Comme la rubrique l'indique, nous sommes censés "nous entraider" non ?
Merci pour ton indulgence @kekia
Re: Maths financières : suites géométriques, annuités
Bonjour,
Après plusieurs calculs j'ai trouvé une annuité/versement mensuel de 342.39.
Cela vient du fait que lorsque j'ai calculé le capital visé (2500€/mensuels) j'ai intégré les 6% d'intérêts et donc le montant de capital nécessaire est de 333653.48.
J'ai utilisé le taux équivalent des 6% annuels soit ==> 0.004868
J'ai utilisé la formule VO = a (1-(1+i)^-n / i pour parvenir au capital avec les intérêts intégrés.
Si quelqu'un pouvait me corriger si cela est faux ?
Merci pour votre aide par avance.
Après plusieurs calculs j'ai trouvé une annuité/versement mensuel de 342.39.
Cela vient du fait que lorsque j'ai calculé le capital visé (2500€/mensuels) j'ai intégré les 6% d'intérêts et donc le montant de capital nécessaire est de 333653.48.
J'ai utilisé le taux équivalent des 6% annuels soit ==> 0.004868
J'ai utilisé la formule VO = a (1-(1+i)^-n / i pour parvenir au capital avec les intérêts intégrés.
Si quelqu'un pouvait me corriger si cela est faux ?
Merci pour votre aide par avance.
Re: Maths financières : suites géométriques, annuités
Bonsoir
En prenant le taux équivalent de 6 % l'an égal à 0.004867550565 pour 1 mensuel on trouve un capital d'origine égal à 333 666,903 euros que je vous laisse arrondir.
Je vous laisse continuer le montant mensuel de capitalisation en précisant la formule que vous appliquez.
En prenant le taux équivalent de 6 % l'an égal à 0.004867550565 pour 1 mensuel on trouve un capital d'origine égal à 333 666,903 euros que je vous laisse arrondir.
Je vous laisse continuer le montant mensuel de capitalisation en précisant la formule que vous appliquez.
Re: Maths financières : suites géométriques, annuités
Bonjour à tous,
La bonne réponse est bien 342,39€, mais dans un exercice comme celui-ci, il est tout à fait inutile et même contre-productif de passer par le calcul du taux équivalent mensuel, lequel s'élimine dans l'équation d'équivalence des flux réciproques.
La simple application du principe d'équivalence des flux réciproques à la date du dernier versement de "Monsieur Jean" conduit directement à une équation permettant de dégager le montant des versements d'épargne à prévoir demandé dans ce problème.
C'est cette résolution qui constituera le traitement "élégant" de cet exercice que Ricu57 appelle de ses vœux
Je manque de temps dans l'immédiat..
Je reviens dès que j'ai un peu de temps.
Bien cordialement à tous..
Alex321
La bonne réponse est bien 342,39€, mais dans un exercice comme celui-ci, il est tout à fait inutile et même contre-productif de passer par le calcul du taux équivalent mensuel, lequel s'élimine dans l'équation d'équivalence des flux réciproques.
La simple application du principe d'équivalence des flux réciproques à la date du dernier versement de "Monsieur Jean" conduit directement à une équation permettant de dégager le montant des versements d'épargne à prévoir demandé dans ce problème.
C'est cette résolution qui constituera le traitement "élégant" de cet exercice que Ricu57 appelle de ses vœux
Je manque de temps dans l'immédiat..
Je reviens dès que j'ai un peu de temps.
Bien cordialement à tous..
Alex321
Re: Maths financières : suites géométriques, annuités
Comme déjà mentionné dans mon précédent post, il n’est pas judicieux de passer par le calcul du taux équivalent mensuel, de même qu’il est inutile de calculer la valeur actuelle de la rente ou la valeur acquise par les versements d’épargne à la date du dernier d’entre eux.
L’équation d’équivalence des flux réciproques à cette date s’écrit directement :
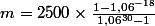
Ce qui donne :
m = 342,39€
Bien cordialement.
Alex321
L’équation d’équivalence des flux réciproques à cette date s’écrit directement :
Ce qui donne :
m = 342,39€
Bien cordialement.
Alex321
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
