Longueur de médianes

par **yos** » 10 Mar 2007, 12:26

Bonjour.
Quant on calcule les longueurs a', b', c' des médianes d'un triangle de côtés a, b, c, on a facilement les relations

,

.
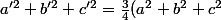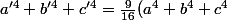J'ai un livre d'exos (Moisotte, prépa capes) où on demande de prouver l'existence d'une suite

de rationnels telle que

.
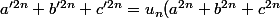Je pense que c'est faux au delà de n=2. J'imagine qu'il faut comprendre que

est indépendant du triangle comme dans les cas n=1 et n=2.
Voilà, si quelqu'un est motivé pour regarder ce problème...

par **fahr451** » 10 Mar 2007, 12:45

bonjour yos

moisotte prépa capes c'est tout une époque ...

par **yos** » 10 Mar 2007, 13:33

Salut Fahr.
Oui c'est l'époque où l'un des deux oraux du capes maths consistait à recevoir un exo comme celui-ci au tableau et à le traiter devant le jury sans préparation. L'essentiel était de pas rester bouche bée (et de pas dire trop de conneries). Ce livre renferme 1850 exercices de ce type et c'est une vraie mine pour fabriquer des problèmes pour le lycée.

par **Blueberry** » 10 Mar 2007, 15:40

Bonjour,

A partir de l'égalité a'^2 = a^2/2+b^2/2 - c^2/4

on obtient en élevant à la puissance n pour a', b' et c' quelquechose de la forme :

vn*a^2n + wn*b^2n+xn*c^2n

a, b et c jouant des rôles symétriques, vn = wn = xn d'où l'existence d'une suite de rationnels telle que

a'^2n + b'^2n + c'^2n = un(a^2n + b^2n + c^2n)

par **fahr451** » 10 Mar 2007, 20:21

bonsoir yos
aurais-tu une version expurgée?

1932 exercices chez moi

exercice n°5 page 80 chap 10 section 11 pour ton exo

par **yos** » 10 Mar 2007, 20:30

Pas expurgée mais un peu plus ancienne je crois (1978).
Mais c'est bien page 80, exo 5 section 11.
J'imagine que les 82 exos supplémentaires sont à la fin??

par **fahr451** » 10 Mar 2007, 20:38

en effet

section exos supplémentaires pour la 2ieme édition donnés depuis 1978 qu 'il dit

par **yos** » 13 Mar 2007, 17:26

Bon ben j'essaie "lesmathematiques.net".

Longueur de médianes

longueur de médianes

Qui est en ligne