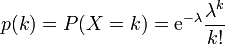Loi de poisson
13 messages
- Page 1 sur 1
loi de poisson
salut
quelqu'un pourrait m'expliquer la loi de poisson(en probalité) dans le cas des files d'attentes ?comment obtenir le nombre de clients arrivant a une file d'attente selon cette loi ?
merci
quelqu'un pourrait m'expliquer la loi de poisson(en probalité) dans le cas des files d'attentes ?comment obtenir le nombre de clients arrivant a une file d'attente selon cette loi ?
merci
bonjour
on montre en fait sous certaines hypothèses convenables que la loi de poisson régit le nombre d'arrivées pendant une durée donnée
mais là il suffit de comprendre
{X=k} est l'événement il y a k arrivées, p(k) est la proba de cet événement
il faut apprendre le cours sur les lois discrètesde poisson ou non.
on montre en fait sous certaines hypothèses convenables que la loi de poisson régit le nombre d'arrivées pendant une durée donnée
mais là il suffit de comprendre
{X=k} est l'événement il y a k arrivées, p(k) est la proba de cet événement
il faut apprendre le cours sur les lois discrètesde poisson ou non.
voici les hypothèses
1 le nombre d'arrivées dans un intervalle de temps donné ne dépend que de l'amplitude de l'intervalle, il est nul si l'amplitude est nulle
2 les arrivées sont indépendantes dans des intervalles [u,u+t] et [u+t,u+t+s]
u,t,s positifs
3pour n quelconque Pn(t) proba qu'il arrive n personnes dans [0,t] est une fonction dérivable par rapport à t
4 [ 1 - P0(t) ]/ P1(t) - > 1 quans t -> 0+
1 le nombre d'arrivées dans un intervalle de temps donné ne dépend que de l'amplitude de l'intervalle, il est nul si l'amplitude est nulle
2 les arrivées sont indépendantes dans des intervalles [u,u+t] et [u+t,u+t+s]
u,t,s positifs
3pour n quelconque Pn(t) proba qu'il arrive n personnes dans [0,t] est une fonction dérivable par rapport à t
4 [ 1 - P0(t) ]/ P1(t) - > 1 quans t -> 0+
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :