Loi normale, grosse incompréhension

[juju78]

Bonjour, je viens de commencer cette loi et je ne comprends pas cet exo


La variable aléatoire X suit une loi normale

Calculez pour m=3 et \sigma=2 P(X < 3,5)

La prof a ecrit:

X ~ N(3,2)

~ N(0,1)

P(X < 3,5) =



=P(Y <

=P(Y < 0,25)= 0,5987

Comment passe t-on de

P(.Y + m < 3,5)

à


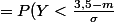puis à P(Y < 0,25)= 0,5987 ??

[COTLOD]

On a les équivalences :



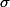
Ensuite les valeurs de m et de sont utilisées.
Pour la fin, il existe des tables de loi normale (centrée réduite), des méthodes d'approximation pouvant être effectuées par des machines...

[juju78]

En fait la seule chose que je n'ai pas compris c'est

P(Y < 0,25)= 0,5987

comment trouve ton 0,5987? avec un tableau?

[COTLOD]

Oui ça existe. Une valeur de P(Y<b) est une intégrale de à b le la fonction de densité .
Il y a la méthode du point milieu, du trapèze, etc... pour en donner une approximation. Cela prend du temps.

[john32]

N'y aurait t'il pas plutôt une racine(sigma) qui traine a la place du simple sigma au dénominateur.
Ce qui compte c'est de normalliser les données donc numérateur et dénominateur doivent avoir la même unité je pense