Localisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 26 Déc 2013, 20:29
par zork » 26 Déc 2013, 20:29
Bonsoir,
Soit un anneau A=Z/6Z et S une partie multiplicative de A:S={1,2,4}
pour trouver
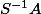
j'ai fais la méthode bourrin mais j'y suis arrivé.
Est-il possible de connaitre d'avance le nombre d'éléments de
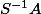
sans calcul explicite des éléments?
merci
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Déc 2013, 20:54
par barbu23 » 26 Déc 2013, 20:54
Bonsoir : :happy3:
Si je ne m'abuse, théoriquement :
On note

l'image réciproque de

par la surjection canonique :

.
Alors :
 \simeq S^{-1} \Big( \mathbb{Z} / 6 \mathbb{Z} \Big) $)
.
Cordialement. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Déc 2013, 21:05
par barbu23 » 26 Déc 2013, 21:05
Bonsoir : :happy3:
Si je ne m'abuse, théoriquement :
On note

l'image réciproque de

par la surjection canonique :

.
Alors :
 \simeq S^{-1} \Big( \mathbb{Z} / 6 \mathbb{Z} \Big) $)
.
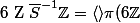 \rangle $)
: idéal de

engendré par :
 $)
.
Cordialement. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Déc 2013, 21:11
par barbu23 » 26 Déc 2013, 21:11
Bonsoir : :happy3:
Si je ne m'abuse, théoriquement :
On note

l'image réciproque de

par la surjection canonique :

.
Alors :
 \simeq S^{-1} \Big( \mathbb{Z} / 6 \mathbb{Z} \Big) $)
.
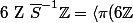 \rangle $)
: idéal de

engendré par :
 $)
.
Cordialement. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Déc 2013, 21:17
par barbu23 » 26 Déc 2013, 21:17
Bonsoir : :happy3:
Si je ne m'abuse, théoriquement :
On note

l'image réciproque de

par la surjection canonique :

.
Alors :
 \simeq S^{-1} \Big( \mathbb{Z} / 6 \mathbb{Z} \Big) $)
.
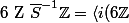 \rangle $)
: idéal de

engendré par :
 $)
.

.
Cordialement. :happy3:
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 26 Déc 2013, 21:20
par zork » 26 Déc 2013, 21:20
oui j'ai un truc comme ca dans le cours
mais pi(6Z) c'est quoi?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Déc 2013, 21:21
par barbu23 » 26 Déc 2013, 21:21
J'ai corrigé, désolé. :happy3:
 $)
est l'image de l'idéal

, par le morphisme :
 = \frac{a}{1} $)
.
Parce que, l'image d'un idéal par un morphisme n'est pas forcément un idéal, c'est pourquoi on prend l'idéal engendré. :happy3:
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 27 Déc 2013, 20:15
par zork » 27 Déc 2013, 20:15
je pose A=Z I=6Z et S={1,2,4} et S*={1*,2*,4*}
dans mon cours on me dit que :

isomorphe à
/(S^{-1}I))

Mais que vaut

?
si je fais le calcul:

mais à ce moment là suivant que je considère 6 comme 3x2 ou 2x3 je peux avoir le choix entre 2 choses: I=3Z ou I=2Z
Comment choisir?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Déc 2013, 20:47
par barbu23 » 27 Déc 2013, 20:47
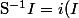 S^{-1} A = IS^{-1} A = \langle i ( I ) \rangle $)
avec :

défini par :
 = \frac{a}{1} $)
.
Cordialement. :happy3:
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 27 Déc 2013, 20:54
par zork » 27 Déc 2013, 20:54
en faite je veux montrer que:
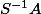
est isomorphe à Z/3Z
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Déc 2013, 21:05
par barbu23 » 27 Déc 2013, 21:05
zork a écrit:en faite je veux montrer que:
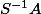
est isomorphe à Z/3Z
Je suis désolé, je ne peux pas t'aider dans cet exo, parce que, je ne me suis jamais entrainé à faire des exos la dessus, je connais la théorie sans connaitre la pratique. :hum: :zen:
J'aurai aimé t'aider, mais, je ne peux pas. :happy3:
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 28 Déc 2013, 13:46
par zork » 28 Déc 2013, 13:46
je regarde cela
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
est isomorphe à Z/3Z