Limite d'une suite de racines complexes

par **charlie12** » 15 Juil 2007, 01:48

bonsoir à tous

voici un problème qui a quelques années, pour lequel je n'ai toujours aucune solution RIGOUREUSE. je vous le livre en entier (il provient d'un ancien journal lemonde rubrique mathématique). Si quelqu'un connaît la réponse, merci de m'en faire profiter ! à bientôt !

PRELIMINAIRES:
Soit A = racine ( -1/4 + racine ( -1/4 + racine (-1/4 .....)))
(pas de pb de définition, voir plus bas)
pour trouver A, on met au carré et on trouve
Acarré = -1/4 + A
On factorise : (A - 1/2) (A - 1/2) =0 d'où A = 1/2

LE PROBLEME :
soit B = racine ( -3/16 + racine ( -3/16 + racine (-3/16 .....)))
Bcarré = -3/16 + B
on factorise : (B - 1/4 ) (B - 3/4) = 0 d'où B=1/4 ou 3/4

On aurait donc DEUX solutions possibles : LAQUELLE EST LA BONNE ? POURQUOI ?

NB :
cet énoncé n'a pas de problème de définition, car bien qu'une racine d'un complexe ne soit pas définie mathématiquement, il suffit de définir
racine d'un complexe = racine de [ r*exp(i*teta) ] = racine(r) * exp (i*teta/2).
Donc je prends (à tort ?) cet énoncé plus pour un abus de notation qu'une erreur véritable.

sinon voici une formulation plus orthodoxe :
soit (bn) la suite définie par
b0=0
bn+1 est tel que bn+1 carré = - 3/16 + bn AVEC arg(bn) dans [0;pi[
prouver que bn converge et donner sa limite.

Merci à tous ceux qui voudront bien y passer du temps ... pour me/le comprendre !

par **cesar** » 15 Juil 2007, 06:53

combien y a t il de nombres complexes dont le carré donne -3/16 ?.....
et puis c'est quoi racine d'un nombre complexe ? en nombre reel on sait, mais en complexe ?

par **charlie12** » 15 Juil 2007, 08:34

bonjour cesar !

que penses-tu du raisonnement suivant ?
il y a exactement 2 nb dont le carré est -3/16 : -3i/16 et +3i/16

plus généralement, il y a toujours 2 nb dont le carré est un complexe donné:
si ton complexe vaut r*exp(i*teta) (teta dans [0,2pi[ ), alors les 2 nb dont le carré vaut ce complexe sont :
racine(r)*exp(i*teta/2) et racine(r)*exp(i*(teta/2+pi) (c'est à dire l'opposé du premier)

Et pour avoir un résultat unique, prenons, comme définition de la racine d'un complexe, la solution dont l'argument est dans [0,pi[

ça semble rigoureux, non ?

par **alben** » 15 Juil 2007, 11:25

Bonjour,
De manière générale, si une suite récurrente vérifie

, on peut toujours essayer de résoudre l'équation L=f(L) qui va donner p solutions.
Cela permet de connaitre les nombres candidats à être limite. Mais sans aucune garantie, il est possible que la suite ne converge pas, que plusieurs des solutions soient valeurs d'adhérence ou aucune, que tout soit déterminé par les premiers termes etc...
Dans ton exemple, tes suites ne sont pas "calculables" car il faudrait pouvoir commencer le calcul, c'est à dire choisir quelle racine complexe de -3/16 on va prendre. C'est une question délicate liée à la determination continue du log dans C.
En prenant la determination arg[0,pi[ comme tu le proposes ça va marcher et la limite sera 3/4
D'ailleurs en prenant l'autre racine ce sera la même limite.

par **cesar** » 15 Juil 2007, 14:12

alben a écrit:. C'est une question délicate liée à la determination continue du log dans C..

elle existe cette determination : on prend l'angle argument dans ]-pi,+pi[

alben a écrit:.
En prenant la determination arg[0,pi[ comme tu le proposes ça va marcher et la limite sera 3/4 ..

qu'est ce qui vous permet de dire cela ?

par **alben** » 15 Juil 2007, 14:24

Suite
En y réflichissant l'expression
A = racine ( -1/4 + racine ( -1/4 + racine (-1/4 .....)))
n'a pas de sens mathématiquement. Il faut préciser ce que veulent dire les points de suspension. C'est la source de l'ambiguïté rencontrée
En revanche, on peut définir une suite

avec u0 > 3/16 (cette dernière condition n'est pas utile si l'on raisonne dans C)
Alors la limite A de la suite sera 3/4 pour toute valeur sauf u0=1/4 pour laquelle la suite est constante.
On peut s'en convaincre ainsi :
si

alors

alors que si

alors

PS je n'ai pas démontré que pour tout u0 dans C la suite est convergente. Ca doit être faisable mais il fait trop chaud

@cesar : la formule avec les points de suspension suppose que l'on calcule en commençant quelque part et donc de calculer des racines. On convient dans R que le signe racine correspond à la racine positive mais cette convention ne s'applique plus dans C et l'on a deux racines dans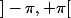

. D'où la limitation par charlie à un demi plan.

par **quinto** » 15 Juil 2007, 15:59

cesar a écrit:elle existe cette determination : on prend l'angle argument dans ]-pi,+pi[

Justement non puisque pour un argument de pi, on ne le défini pas.

par **emdro** » 15 Juil 2007, 16:20

Que dites-vous du raisonnement simple suivant:

?

On ne rique rien avec i, mais il faut se méfier des racines de nombres négatifs!

par **nuage** » 15 Juil 2007, 17:13

Salut,
si on prend en compte toutes les racines, après 11 itérations on a ça :

par **alben** » 15 Juil 2007, 17:38

Bonsoir nuage
C'est très joli ce nimbus mais un peu narcissique, non ?

par **nuage** » 15 Juil 2007, 18:02

alben a écrit:Bonsoir nuage
C'est très joli ce nimbus mais un peu narcissique, non ?

Je ne l'avais pas vu comme ça, mais, en effet, je suis assez narcissique :happy:
Pour rajouter un peu de maths :
Je pense qu'on a un ensemble fractal sur lequel convergent toutes les racines, quelque soit

.
Mais c'est juste une impression lié à des expériences numériques.

par **charlie12** » 15 Juil 2007, 20:05

tout d'abord, MERCI A TOUS DE VOUS ETRE INTERESSE A CE PB !

ma définition de la racine doit être changée, prenons exemple sur la ... calcultrice !

Lorsqu'on tape une racine d'un complexe r*e(iT) sur une calculatrice, elle nous donne un seul résultat: racine(r)*e(iT/2) pour T dans ]-pi,pi] (et non 0,2pi ) (un peu comme un cos-1 qui ne donne qu'un seul résultat)

donc EMDRO, la formule racine(x)*racine(y)=racine(x*y) ne serait valable QUE SI l'argument de x*y reste dans l'intervalle ]-pi,pi]
avec cette correction le contre-exemple avec -1 n'en est plus un car racine(-1)*racine(-1)=racine (eipi)*racine(eipi) = STOP = car argument du produit = 2pi. Il doit y avoir matière à creuser pour étendre la def, mais LIMITONS LA A CE QUE RENVOIE LA CALCULATRICE

pour ce problème, j'avais déjà essayé une piste géométrique (un peu comme NUAGE mais en moins joli!) : l'effet de la racine de la calculatrice sur un
complexe est : sur la bissectrice de l'angle entre l'axe xx' et l'axe OM (M point d'affixe le complexe en question), on place le point M' tq OM'=racine de OM

DONC l'algorithme de construction des points de la suite serait :
on place -3/16
BOUCLE
on trace la bissectrice de l'angle xOM
on place M' dessus pour que OM'=racine de OM
on translate horizontalement le pt obtenu de -3/16*vecteur abscisse (je n'ose pas mettre i !)
on REBOUCLE

visuellement (pas tres rigoureux ça!) ça tend bien vers l''abscisse , mais pourquoi vers 3/4 ? (réponse de la calculatrice par ce procédé)

qu'en pensez vous ?

par **cesar** » 15 Juil 2007, 21:35

quinto a écrit:Justement non puisque pour un argument de pi, on ne le défini pas.

si le log complexe existe : c'est un intervalle ouvert en pi, sinon il y aurait des log de nombres négatifs

http://fr.wikipedia.org/wiki/Logarithme_complexe

par **cesar** » 15 Juil 2007, 21:38

emdro a écrit:Que dites-vous du raisonnement simple suivant:
?

On ne rique rien avec i, mais il faut se méfier des racines de nombres négatifs!

j'en dis que cette relation est fausse...
la vraie est :

ou

par **nuage** » 15 Juil 2007, 21:55

Juste une remarque sur la définition de la racine carrée > :
en général on prend les arguments de départ sur

et l'argument de la racine carrée est pris sur

plutôt que sur

par **quinto** » 15 Juil 2007, 23:45

cesar a écrit:si le log complexe existe : c'est un intervalle ouvert en pi, sinon il y aurait des log de nombres négatifs

http://fr.wikipedia.org/wiki/Logarithme_complexe

C'est exactement ce que je te dis.
Et note que l'on peut avoir des ln de nombres négatifs. Le problème se pose si l'on oublie d'enlever à C, une courbe simple qui relie 0 à l'infini.

Limite d'une suite de racines complexes

limite d'une suite de racines complexes

Qui est en ligne