Leçon 63 CAPES

[jeje56]

Bonjour,

Je prépare la leçon 63 qui s'intitule : "Fonction réciproque d'une fonction strictement monotone sur un intervalle de R. Etude de la continuité, de la dérivabilité. Exemples".

J'ai plusieurs supports : par exemple, est-ce légitime de définir dans un premier temps la notion d'inversibilité d'une fonction pour parler de réciproque ?

D'autre part, j'ai vu dans un livre énoncé le théorème de la limite monotone pour les fonctions... Est-ce vraiment dans le sujet ? Je trouve qu'il n'a pas vraiment sa place ici...

Si quelqu'un a un ou plusieurs liens vers le sujet ?...

Merci bcp !

[AlexisD]

Je ne sais pas si ca peut t'être utile mais j'ai trouvé ce lien:

http://astroplus.perso.neuf.fr/capes/Lecon65.pdf

Sur ce site, toutes les leçons pour l'oral du CAPES y sont présentes.
Bonne chance en tout cas !

[jeje56]

Merci ! :-)

[mathelot]

Bonjour,


quelques remarques:


i) le fait que soit bijective est "purement algébrique",ie,
cela signifie que l'équation d'inconnue x (y fixé)

f(x)=y

a une unique solution
en général, résoudre cette équation donne le domaine de définition de g et une formule pour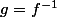

exemples: cos,sin,tan,ch,sh,th,exp,ln,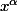, sur des intervalles privilégiés



ii) la stricte monotonie sur l'intervalle est une condition nécessaire et suffisante lorsque f est continue.
du coup, on récupère facilement la continuité du fait que f étant par exemple
strictement croissante, est un morphisme d'ordre , conserve la relation d'ordre
et envoie localement un intervalle sur un intervalle, ce qui est pratiquement la définition de la bi-continuité

on parle alors d'homéomorphisme

iii) il y a des exemples de bijections continues non bicontinues. Il faut sortir du cadre des espaces vectoriels complets (Banach) et exhiber
un contre-exemple dans un espace topologique (exemple: la fonction identité
entre l'espace muni de sa topologie grossière et à l'arrivée de sa topologie discrète)

iv) la surjectivité d'une application continue strictement croissante provient
via le TVI, du fait que l'ensemble des réels est un "continuum", un espace connexe, sans trous. ce qui n'est nullement évident.

Du point de vue visuel,les nombres sont bien assimilés à la droite géométrique.
mais le fait que R soit un "continuum" provient, lors de la construction par les suites de Cauchy , de la complétion, ce qui fait appel à la notion d''infini et de limite, soit par la construction des nombres avec les "coupures" de Dedekind, d'une sorte de tour de passe-passe:
On définit un nombre comme une "coupure", un trou
exemple

et on récupère un ensemble connexe du fait que l'on a réunit toutes les "coupures" possibles en un ensemble. :zen:
il y a quand même des interrogations à ce sujet, qui transpirent dans l'interrogation récurrente, sur les fora de maths, de savoir si 0,99999999... est bien égal à 1 ou non. :zen:

une façon de sentir que ce "continuum" n'est nullement évident, c'est de se souvenir que l'hypothèse du continu (Cantor) est indémontrable

voilà les interrogations qui se cachent derrière la surjectivité d'une fonction continue strictement monotone.

v)
il y a la notion de morphisme (algébrique) qui fait que si
f est un morphisme ,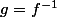 itou
exponentielle-logarithme, puissances et racines
vi)
voici des thèmes que tu peux aborder à l'exposé
- DL et DSE de
en particulier, le dévloppement en série de Taylor de la tangente,
fonction localement inversible , est particulièrement intéressant

- dérivée n-ième de gof (bon courage !)
- théorème d'inversion et fonctions implicites qui est une généralisation
du théorème de la bijection à plusieurs variables
- bijections définies par des intégrales
exemple

L'inversion des fonctions définit par des intégrales constituent
le début de la théorie des fonctions elliptiques