Isomorphie

par **capitaine nuggets** » 09 Oct 2014, 13:05

Bonjour, je voudrais montrer que

est isomorphe à un certain groupe

à préciser (d'après mes recherches, je pense qu'il s'agit de

, mais j'ai un peu de mal.

Voici ce que je sais :
Pour un morphisme de groupes

:
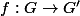
1)

induit un morphisme de groupe injectif

;
2)

induit un isomorphisme de groupes

.

Du coup, je me donne

tel que

. Mais j'ai du mal à déduire quelque chose de cette hypothèse...

Une idée ? :we:

par **arnaud32** » 09 Oct 2014, 13:51

regarde du cote du theoreme des restes chinois

par **capitaine nuggets** » 09 Oct 2014, 14:05

arnaud32 a écrit:regarde du cote du theoreme des restes chinois

Je ne l'ai pas encore vu malheureusement...

par **jlb** » 09 Oct 2014, 14:18

Salut, considère n'importe quel élément (a,b) de ZxZ/4Zx6Z et calcule alors la classe de (12a,12b).
Tu en conclus quoi sur l'ordre de (a,b)? C'est possible qu'il engendre un groupe isomorphe à Z/24Z?

par **capitaine nuggets** » 09 Oct 2014, 14:27

La classe de

est la même que la classe de

.
Autrement dit,

donc l'ordre de

divise

.
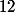
Donc il ne peut pas engendré un groupe d'ordre supérieur à 12

par **jlb** » 09 Oct 2014, 14:30

capitaine nuggets a écrit:La classe de est la même que la classe de .
Autrement dit, donc l'ordre de divise .
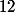
Donc il ne peut pas engendré un groupe d'ordre supérieur à 12

donc tu en déduis quoi sur ton intuition?

par **jlb** » 09 Oct 2014, 14:30

capitaine nuggets a écrit:La classe de est la même que la classe de .
Autrement dit, donc l'ordre de divise .
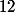
Donc il ne peut pas engendré un groupe d'ordre supérieur à 12

Ok il faut donc revoir ton intuition, non?

par **capitaine nuggets** » 09 Oct 2014, 14:32

jlb a écrit:Ok il faut donc revoir ton intuition, non?

Ouaip, du coup je pense qu'il est plutôt isomorphe à

.

par **jlb** » 09 Oct 2014, 14:34

capitaine nuggets a écrit:Ouaip, du coup je pense qu'il est plutôt isomorphe à .

euh, tu as combien d'éléments dans chaque groupe à "comparer"

par **capitaine nuggets** » 09 Oct 2014, 14:37

jlb a écrit:euh, tu as combien d'éléments dans chaque groupe à "comparer"

Je ne sais pas... j'ai un peu de mal à voir ce que représente

par **jlb** » 09 Oct 2014, 14:40

capitaine nuggets a écrit:Je ne sais pas... j'ai un peu de mal à voir ce que représente

ben, je dirai que ton exo c'est de montrer que c'est isomorphe à Z/4ZxZ/6Z ( j'espère ne pas te raconter n'importe quoi ni t'induire en erreur, je te laisse entre les mains de personnes plus compétente!!).

(a,b) appartient à la classe de (e,f) cela signifie quoi?
(a,b)-(e,f) appartient à ... et tu déroules.

par **capitaine nuggets** » 09 Oct 2014, 14:49

jlb a écrit:ben, je dirai que ton exo c'est de montrer que c'est isomorphe à Z/4ZxZ/6Z ( j'espère ne pas te raconter n'importe quoi ni t'induire en erreur).

Utilise la définition d'un groupe quotient : (a,b) appartient à la classe de (e,f) cela signifie quoi?

Ah j'y avais pensé en considérons l'application :

Je pense que mon erreur aura été de croire que

est isomorphe à

par **Ben314** » 09 Oct 2014, 14:56

De toute façon, tu montre quasiment aussi vite que, si G et G' sont deux groupes et H,H' des sous groupes distingués respectivement de G et. G' alors HxH' est distingué dans GxG' et le quotient (GxG')/(HxH') est isomorphe à (G/H)x(G'/H').

Je sais même pas si ça pourrait pas éventuellement s'appeler un des "théorèmes d'isomorphismes classiques"

par **capitaine nuggets** » 09 Oct 2014, 14:59

Ok, mais du coup, je pars d'où parce que vous m'avez perdu avec toutes vos suggestions :we:

par **Ben314** » 09 Oct 2014, 15:01

Tu part de f : GxG' -> (G/H)x(G'/H') ; (x,y) -> (cl(x),cl(y))
Elle est (trivialement) surjective et son noyau est (trivialement) HxH' donc elle induit un isomorphisme de (GxG')/(HxH') sur (G/H)x(G'/H')

par **capitaine nuggets** » 09 Oct 2014, 15:05

Ben314 a écrit:Tu part de f : GxG' -> (G/H)x(G'/H') ; (x,y) -> (cl(x),cl(y))
Elle est trivialement surjective et son noyau est HxH' donc ç'est bon.

Quand tu me dis que c'est bon, tu veux dire qu'hormis montrer que Ker(f)=HxH' et que f est évidemment surjective, il n'y a rien à faire ?
Ah oui, parce que si f est surjective, alors Im(f)=(G/H)x(G'/H') d'où "l'induction" de l'isomorphisme de GxG'/Ker(f) dans Im(f)=(G/H)x(G'/H').

Ai-je bon ?

par **Ben314** » 09 Oct 2014, 15:12

oui, c'est bon.
Dans le cas où G et G' sont non commutatifs, il faudrait aussi montrer que HxH' est normal dans GxG', mais c'est de nouveau évident...

par **capitaine nuggets** » 09 Oct 2014, 15:15

Ben314 a écrit:oui, c'est bon.
Dans le cas où G et G' sont non commutatifs, il faudrait aussi montrer que HxH' est normal dans GxG', mais c'est de nouveau évident...

Normal signifie-t-il distingué ?
Juste une question : tout sous-groupe d'un groupe abélien est abélien et distingué, n'est-ce pas ?

par **Ben314** » 09 Oct 2014, 15:21

capitaine nuggets a écrit:Normal signifie-t-il distingué ?

Oui, on dit aussi, (mais plus rarement) "sous groupe invariant"

tout sous-groupe d'un groupe abélien est abélien et distingué, n'est-ce pas ?

Oui : dans un groupe commutatif,

donc tout sous groupe est distingué (et évidement commutatif)

Rappel : H est normal dans G ssi

par **capitaine nuggets** » 09 Oct 2014, 15:25

Merci à toi et aux autres pour votre précieuse aide :+++:

Isomorphie

isomorphie

Qui est en ligne