Isométries vectorielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 10:47
par jeje56 » 30 Nov 2008, 10:47
Bonjour,
Je bloque sur l'exercice suivant :
Soit
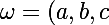)
un vecteur non nul de

et A la matrice

1) Vérifier que

et
^{-1})
commutent : ok
2) Soit R l'endomorphisme de E de matrice
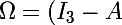(I_3+A)^{-1})
dans la base canonique :
MQ R est une rotation de E qui n'est pas l'identitéJe ne vois pas comment procéder : un calcul du det de

serait trop compliqué je pense...
Merci bcp de votre aide !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 11:49
par jeje56 » 30 Nov 2008, 11:49
=\Omega^{-1})
J'avoue ne pas voir ce que l'on peut en tirer...
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 12:04
par jeje56 » 30 Nov 2008, 12:04
Merci, mais oui je l'ai bien vu tout ça ;-) c'est la suite, que puis-je en tirer... ?
Merci !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 12:30
par jeje56 » 30 Nov 2008, 12:30
On en vient à :
\Omega=I_3)
c'est bien ça ? Ce qui prouve que R est une isométrie...
D'autre part

donc R est une rotation...
Que faut-il dire pour affirmer que R n'est pas l'identité ? (

?...)

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 30 Nov 2008, 12:36
par fourize » 30 Nov 2008, 12:36
bonjour
tout d'abord un petit rappel du cours.
une matrice est dit orthogonale si et seulement si

;
en consequent det(A)=+ou - 1 .
en outre si det(A)=1 c est une rotation.
il reste a determiner l'angle de rotation .
en appliquant ce :++: rappel sur ta matrice tout devait marcher .
* In God we trust, for all others bring data *
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 14:31
par jeje56 » 30 Nov 2008, 14:31
Merci, j'ai compris la première partie.
Pour la suite :
Soit
)
défini par :
=\omega Vx)
où V représente le produit vectoriel
J'ai déterminé la matrice de

dans la base canonique de E :

D'où :
o(Id+u_\omega)^{-1}) On me demande de déterminer l'axe de R
On me demande de déterminer l'axe de R :
ici j'hésite : calculer Ker(R-Id) me semble beaucoup trop long (je n'ai pas calculé explicitement

)
Merci bcp de votre aide !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 16:25
par jeje56 » 30 Nov 2008, 16:25
Personne ?...
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 17:21
par jeje56 » 30 Nov 2008, 17:21
Je tombe sur :
Pour tout x, -2u(x)=0 ssi u(x)=0
C'est juste ?
Merci bcp à toi ;-)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 30 Nov 2008, 17:41
par jeje56 » 30 Nov 2008, 17:41
Ok, merci à toi Angélique !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités