Bonne chance..
Isométries de R^n pour des normes exotiques
9 messages
- Page 1 sur 1
Isométries de R^n pour des normes exotiques
On se fixe un p dans  différent de 2, et on munit
différent de 2, et on munit  de la norme
de la norme 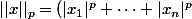^{1/p}) si
si  ,
, 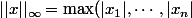) si
si  ( les
( les  étant les coordonnées de
étant les coordonnées de  ). Caractérisez les isométries linéaires de
). Caractérisez les isométries linéaires de ) dans lui même.
dans lui même.
Bonne chance..
Bonne chance..
Vu que, si p est différent de 2, la norme en question n'est pas issue d'un produit scalaire, je ne pense pas que le vocable "automorphismes orthogonaux" soit bien adapté...egan a écrit:Il faut bien déterminer les automorphismes orthogonaux c'est ça ?
Edit : La question est interessante est assez naturelle. Je conjecturerais bien que le groupe des isométries est trés petit, voir même réduit à {Id,-Id}...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Le problème revient à chercher les applications linéaires bijectives qui stabilisent la boule unité (pour cette norme).
Vu la tronche peu symétrique des boules (principalement pour p=1 et p=+oo) je pense que le groupe des isométries est isomorphe à Snx(Z/2Z)^n (permutation des coordonnées et changement de signe de certaines coordonnées) (ce qui légèrement plus gros que ma première intuition)
Vu la tronche peu symétrique des boules (principalement pour p=1 et p=+oo) je pense que le groupe des isométries est isomorphe à Snx(Z/2Z)^n (permutation des coordonnées et changement de signe de certaines coordonnées) (ce qui légèrement plus gros que ma première intuition)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
