Isometries

[barbu23]

Bonsoir à tous : :happy3:
J'ai quelques petites questions à vous poser concernant les types d'isometries qui existent en algèbre et géometrie :
Que signifie une isometrie "linéaire" et quelle différence y'a-t-il entre une isometrie linéaire et une isométrie vectorielle ou affine par exemple ?
Quelles sont toutes les types d'isometries qui existent en geometrie : je ne connais que deux : la rotation et la translation ?
Est ce que une isometrie ou particulièrement une isometrie vectorielle est toujours definies sur un espace orthonormé ?
Merci d'avance de votre aide ! :happy3:

[Nightmare]

Salut :happy3:

1) Isométrie linéaire? Ce n'est pas courant... Cependant je pense que cela désigne une isométrie vectorielle.

Une isométrie vectorielle c'est simplement un automorphisme orthogonal.

Une isométrie affine c'est une application affine dont la partie linéaire est une isométrie vectorielle.

2) Je suppose que tu parles dans le plan... Et les symétries on les oublie? Et toutes les composées...

3) Un espace orthonormé? Qu'est-ce donc? Pour définir une isométrie vectorielle on a juste besoin d'un produit scalaire, ie d'un espace préhilbertien.

:happy3:

[barbu23]

Merci "Nightmare" pour ces précisions ! :happy3: ça fait longtemps que je jette pas d'oeil sur ce cours de geometrie ... En plus , on ne l'utilise que très rarement dans les autres disciplines mathematiques ! Maintenant, j'applique un peu ces notions en theorie des EDP ! d'ailleurs juste une partie et non pas toute où on dit que le Laplacien et la fonction de Dirac sont invariants par les isometries de l'espace euclidien !
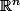
Par contre, c'est quoi une fonction radiale ?

[Nightmare]

Je n'ai rencontré qu'une fois ce terme, si mes souvenirs sont bons c'est une fonction vectorielle qui ne dépend que de la norme du vecteur (par exemple f(x)=||x||+1)

[barbu23]

Oui, voila merci ! :happy2:

[Nightmare]

Je t'en prie :happy3: