Intervalle et segment

[Anonyme]

Bonjour, j'aurai voulu savoir quelle était la différence entre un intervalle fermé et un segment.
Merci d'avance pour la réponse!

[phenomene]

Bonjour, un segment est un intervalle fermé et borné. La notion de fermé t'est peut-être inconnue, cela dépend de ton niveau d'études. Disons qu'un intervalle est fermé si, lorsqu'on a une suite de points de l'intervalle qui converge, alors la limite appartient nécessairement à l'intervalle. On peut aussi dire qu'un intervalle est fermé s'il contient tous ses "points frontière" (mais il faudrait définir cette dernière notion rigoureusement).

Par exemple, est un segment, alors que est un intervalle fermé qui n'est pas borné, ce n'est pas un segment. L'intervalle 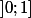est borné mais n'est pas fermé, il ne contient pas son point frontière . Enfin, l'intervalle quant à lui n'est ni fermé, ni borné.

[Anonyme]

ok, j'ai compris.
Merci beaucoup

[Anonyme]

Est ce que vous pouvez me donner un autre intervalle qui est fermé mais pas borné mais sans avoir plus ou moins l'infini.
Dans, l'intervalle [0,+inf[, on peut trouver une suite de point qui converge vers +inf, mais +inf, fait-il partie de l'intervalle?
En fait je crois que mon véritable souci est que je ne comprend pas comment on peut considéré l'intervalle [a,+inf[, ou,]-inf,a] comme intervalle fermé.

En fait, dans mon cours, on a donné comme définition d'un intervalle fermé les ty pes d'intervalles [a,b],[a,inf[,]inf,a].
Et on a aussi considérer que ]-inf,+inf[ était un intervalle fermé mais aussi un intervalle ouvert.
Tout ca n'est pas très clair...

[phenomene]

Dans, l'intervalle [0,+inf[, on peut trouver une suite de point qui converge vers +inf, mais +inf, fait-il partie de l'intervalle?

Bonjour, le symbole ne désigne pas un nombre réel, c'est une simple convention de notation dans ce contexte. Il ne peut donc pas faire partie d'un intervalle réel, c'est pourquoi on note toujours le crochet en l'infini ouvert quand on parle d'intervalle réel. Une suite de nombres réels qui tend vers l'infini n'est pas convergente dans . On dit qu'une suite est convergente dans lorsqu'elle admet une limite réelle, c'est-à-dire finie.

Enfin, attention, fermé n'est pas le contraire d'ouvert, un intervalle peut être à la fois ouvert et fermé comme , ou être ni l'un ni l'autre comme .