Interpolation de lagrange

[muse]

Bonjour,

Voila l'exercice :


il y a juste la dernière question que je n'arrive pas a faire.
Pouvez vous me donner une petite indication.

J'ai penser a dire que
|f(x)-L(x)|=|g(x)+A/2 (x-a)(x-b)|

et la ce serait bien d'avoir g positive enfin d'avoir l'inégalité demandée mais je ne vois pas pourquoi g serait positive donc je ne sais pas.

Merci

[Maxmau]

Bj
Je note x* (au lieu de x chapeau)
Question 2 A est choisie telle que g(x*) =0
Applique Rolle à g entre a et x* puis entre x* et b
Puis Rolle encore une fois à g'

[muse]

ça c'est pour la question trois :) j'ai réussi c'est juste la majoration de l'erreur que je n'arrive pas a faire.

merci

[Maxmau]

ça c'est pour la question trois j'ai réussi c'est juste la majoration de l'erreur que je n'arrive pas a faire.

merci

fais x = x* (x* = x chapeau)
dans l'expression de g ( g(x*) = 0)

[muse]

ha ok facile en fait je suis bete :)
et pour la deuxième majoration ? :)

[Maxmau]

ha ok facile en fait je suis bete
et pour la deuxième majoration ?

Là c'est encore plus bête !!

[muse]

si tu dis que c'est encore plus bête je vais chercher encore.

Une petite indication quand même, Il faut se servir juste de la premiere majoration ?

[leon1789]

Une petite indication quand même, Il faut se servir juste de la premiere majoration ?

quelles sont les différences entre les deux inégalités de cette question ?

[muse]

en fait ce qui m'embete c'est le 8 aprce que on a
(x*-a)(b-x*)
Donc en fait pour avoir le 8 il faudrait que ces inégalité soient vraies en divisant par 2 le b-a mais si c'est vrai pour l'un ça ne l'est pas pour l'autre (d'apres mon petit dessin) donc je ne sais pas :(.


EDIT:
pour répondre a ta question la différence c'est qu'il n'y a plus de x qui traine

[leon1789]

en fait ce qui m'embete c'est le 8 aprce que on a
(x*-a)<b-a
(b-x*)<b-a

ok, mais ces majorations sont trop brutales, comme tu le vois après.

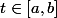
Comment majorer au plus juste le produit (t-a)(b-t) pour ? (étudier la... :id:)

[muse]

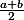
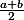
si j'étudie cette fonction je trouve que le max est atteint en et donc si je remplace t par je trouve que

(t-a)(b-t) est majoré par

On se rapproche je continue de réfléchir

EDIT:
pour trouver l'egalité demander il faudrait que (b-a)(b+a)}<(b-a)² mais c'est faux donc j'ai du me tromper quelque part mais j'en ai pas l'impression.
Et je ne peux pas faire une majoration plus "fine" puisque elle est atteinte

[leon1789]

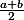
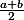
si j'étudie cette fonction je trouve que le max est atteint en et donc si je remplace t par je trouve que

(t-a)(b-t) est majoré par

attention, tu as fait une erreur de signe...
et regarde bien l'énoncé...

[muse]

au tant pour moi j'ai pas developer un signe - donc a bien le resultat:

ce qui donne le bon resultat

Merci je penserais a trouver les meilleurs majorants possibles en étudiant exactement la fonction