Intégration au sens de Lebesgue

[Mathlab]

Bonjour
Voila ma question :
Soit intégrable au sens de Lebesgue:
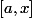
Justifier que est Lebesgue intégrable sur tout interalle où
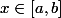
Quelqu'un aurait-il une idée de solution ?
Merci d'avance

[arnaud32]

[Mathlab]

Ok merci bien,
La suite du problème est :
montrer que F est continue.
je ne comprend pas car une fonction en escalier n'est pas continue mais est Lebesgue intégrable

[pascal16]

on ne regarde pas la continuité de la fonction de base, mais celle de son intégrale de a à x.


au sens de Riemann, l'intégrale d'une fonction en escalier est intégrable de a à x et est une fonction affine par morceaux continue.

[arnaud32]

tu peux repartir de la definition de la continuite