Intégration lebesgue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 07 Oct 2014, 21:29
par Guitou80 » 07 Oct 2014, 21:29
Bonjour,
Edit: les données des questions sont maintenant correctesje suis en L3 de maths et je trouve cette UE extrêmement hard. J'ai quelque questions, qui n'ont pas forcément toutes un rapport avec cette matière, qui concernent certains exos :
1. En quoi [0, a[ pour tout a

est un ouvert de

puisque on ne peut mettre une boule centrée en 0 de rayon r>0 ?
2. En quoi
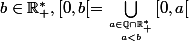
?
Puisque b est soit irrationnel soit rationnel alors que a est toujours rationnel
Merci
-
mathelot
 par mathelot » 07 Oct 2014, 21:33
par mathelot » 07 Oct 2014, 21:33
Guitou80 a écrit:Bonjour,
je suis en L3 de maths et je trouve cette UE extrêmement hard. J'ai quelque questions, qui n'ont pas forcément toutes un rapport avec cette matière, qui concernent certains exos :
1. En quoi [0, a[ est un ouvert de

puisque on ne peut mettre une boule centrée en 0 de rayon r>0 ?
ça risque pas d'être un ouvert de machin, ce n'est pas inclu dedans.
Il faut au minimum que les éléments de la topologie soient des parties de l'espace.2. En quoi si
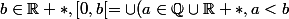 [0, a[)
tester la double inclusionQuelle est svp la syntaxe tex pour mettre
)
sous le
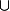
?
Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Oct 2014, 23:19
par Ben314 » 07 Oct 2014, 23:19
Guitou80 a écrit:Quelle est svp la syntaxe tex pour mettre
)
sous le
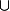
?
[0,b[ = \Bigcup_{a\in{\mathbb Q}\cap{\mathbb R}_+^* \atop a<b} [0,a[

(et a mon avis, entre Q et R*+, c'est une intersection et pas une réunion)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 08 Oct 2014, 09:57
par Guitou80 » 08 Oct 2014, 09:57
Merci pour vos réponses, j'ai corrigé mes erreurs d'énoncé dans mon premier post.
mathelot :

Dans ce sens là c'est trivial même pas besoin de se justifier, en revanche dans l'autre sens c'est plus compliqué car a

b mais ne l'atteint jamais, donc si on compare les cardinaux de ces 2 ensembles

a un élément de plus il me semble
Qu'en pensez-vous ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 08 Oct 2014, 11:05
par arnaud32 » 08 Oct 2014, 11:05
utilises la densite des rationnels dans R
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 08 Oct 2014, 17:55
par Guitou80 » 08 Oct 2014, 17:55
arnaud32 a écrit:utilises la densite des rationnels dans R
Ok merci, et en quoi [0, a[ pour tout a

est un ouvert de

puisque on ne peut mettre une boule centrée en 0 de rayon r>0 ?
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 08 Oct 2014, 20:40
par Guitou80 » 08 Oct 2014, 20:40
Bonsoir,
je ne comprend pas bien cette inclusion ici (point d'interrogation devant la ligne )

Merci de me mettre sur la voie
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 08 Oct 2014, 20:48
par deltab » 08 Oct 2014, 20:48
Bonsoir.
Guitou80 a écrit:Ok merci, et en quoi [0, a[ pour tout a

est un ouvert de

puisque on ne peut mettre une boule centrée en 0 de rayon r>0 ?
Tu parles de boules,
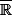
est-il un espace métrique? La topologie prise sur

est la topologie induite par celle de
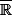
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 08 Oct 2014, 22:39
par Guitou80 » 08 Oct 2014, 22:39
deltab a écrit:Bonsoir.
Tu parles de boules,
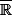
est-il un espace métrique? La topologie prise sur

est la topologie induite par celle de
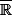
Non c'est un espace topologique, pourquoi cet ensemble est un ouvert ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Oct 2014, 07:46
par arnaud32 » 09 Oct 2014, 07:46
c'est quoi la definition d'une topologie induite?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Oct 2014, 07:48
par arnaud32 » 09 Oct 2014, 07:48
Guitou80 a écrit:Bonsoir,
je ne comprend pas bien cette inclusion ici (point d'interrogation devant la ligne )

Merci de me mettre sur la voie
c'est la contraposee de la proposition precedente
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 15 Oct 2014, 21:06
par Guitou80 » 15 Oct 2014, 21:06
arnaud32 a écrit:c'est quoi la definition d'une topologie induite?
Salut Arnaud
La topologie induite sur une partie F d'un espace topologique E est la topologie sur F dont les ouverts sont les intersections des ouverts de E avec FDonc si j'ai bien compris,
]0,a[

et

et [0, a]

, donc ]0,a[

[0, a] est un ouvert de la topologie induite sur

?
arnaud32 a écrit:c'est la contraposee de la proposition precedente
Merci
-
mathelot
 par mathelot » 15 Oct 2014, 21:20
par mathelot » 15 Oct 2014, 21:20
Guitou80 a écrit:Bonsoir,
je ne comprend pas bien cette inclusion ici (point d'interrogation devant la ligne )

Merci de me mettre sur la voie
bonsoir,
je plussoie Arnaud.
au niveau des sous ensembles d'un ensemble X
si A et B sont des parties de X, définies par des prédicats
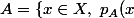 \})
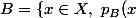 \})
 \Rightarrow p_B(x)))
et

par la contraposée de l'implication précédente (ici la continuité
uniforme)
 \Rightarrow \textrm{ non } p_A(x)))
-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 15 Oct 2014, 21:35
par Guitou80 » 15 Oct 2014, 21:35
Bonjour, pourriez vous svp m'expliquer ce que j'ai souligné en rouge ci-dessous ?

-
Guitou80
- Membre Naturel
- Messages: 19
- Enregistré le: 14 Déc 2011, 18:10
-
 par Guitou80 » 15 Oct 2014, 21:36
par Guitou80 » 15 Oct 2014, 21:36
mathelot a écrit:bonsoir,
je plussoie Arnaud.
au niveau des sous ensembles d'un ensemble X
si A et B sont des parties de X, définies par des prédicats
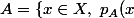 \})
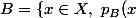 \})
 \Rightarrow p_B(x)))
et

par la contraposée de l'implication précédente (ici la continuité
uniforme)
 \Rightarrow \textrm{ non } p_A(x)))
Merci Mathelot je vais regarder ça
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 15 Oct 2014, 22:30
par mrif » 15 Oct 2014, 22:30
Guitou80 a écrit:Bonjour, pourriez vous svp m'expliquer ce que j'ai souligné en rouge ci-dessous ?

La tribu borélienne
)
est la tribu engendrée par les ouverts de

La tribu borélienne
)
est la tribu engendrée par les ouverts de

Or tout ouvert de

est un ouvert de

donc
 \subset B(\bar R))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités


