Integration cos^2*sin non réussi

[pauldu35]

Bonsoir, cela fait un moment que je bloque sur le calcul de l'intégrale suivante:

I=intégrale cos²(x)*sin(x) borne: pi/4 et 0
Je vous présente mon raissonnement :
intégrations par parties:
u(x)=cos²(x) u'(x)=2cos(x)*(-sin(x))
v'(x)=sin(x) v(x)=cos(x)

I= (cos^3(x)) Borne pi/4 et 0 - Integrale 2*cos(x)*-sin(x)*cos(x) borne Pi:4 et O
I=(V2/2)^3-1 Borne pi/4 et 0 - Integrale 2*cos(x)*-sin(x)*cos(x) borne Pi:4 et O

Cependant je n'arrive pas a primitiver le terme de droite, une petite aide ne serait pas de trop.

Merci de prendre le temps de me répondre.

[girdav]

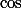
Je regarderai plus tard l'intégration par parties mais il y a plus rapide : on voit que la fonction à intégrer est la dérivée de à une certaine puissance.

[MacManus]

Bonsoir

Attention, v(x) = -cos(x)

Et l'intégrale de droite ressemble fortement à celle de départ...

[pauldu35]

La primitive de sin(x) est bien cos(x) ?

Pourriez-vous m'expliquer votre méthode plus rapide s'il vous plait ?

[MacManus]

La primitive de sin(x) est bien cos(x) ?

Non ! La primitive de sin(x) est -cos(x) (la dérivée de cos(x) est -sin(x))
Pour l'intégrale de droite, tu remarques que son expression est 2*I

[pauldu35]

Oui je suis d'accord, mais malgrès cette erreur, je n'arrive toujours pas avancer. Je reste bloqué au meme point.

[MacManus]

[pauldu35]

Ah oui je n'avais pas corrigé l'erreur qui s'etait glissé dans la première expression . En tout cas, je vous remercie de votre aide.
mais comment determine-t-on la valeur de I par la suite ?

[MacManus]

oui attention au -cos(x) qu'il faut remplacer partout

Eh bien c'est comme une équation du 1er degré à une inconnue.

[pauldu35]

Merci de votre aide.

[MacManus]

As-tu trouvé la valeur de I ?

Sinon l'astuce de "girdav" consiste à écrire cos²(x)sin(x) comme étant la dérivée d'une puissance de "cos".

[MacErmite]

bonjour,

j'ai essayé de calculer cette primitive mais je ne sais pas si cela est correct :

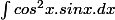
en posant u=cos x de sorte que du=-sin x.dx, ce qui conduit à

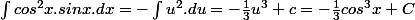
est-ce correct ?

[Black Jack]

Bonsoir, cela fait un moment que je bloque sur le calcul de l'intégrale suivante:

I=intégrale cos²(x)*sin(x) borne: pi/4 et 0
Je vous présente mon raissonnement :
intégrations par parties:
u(x)=cos²(x) u'(x)=2cos(x)*(-sin(x))
v'(x)=sin(x) v(x)=cos(x)

I= (cos^3(x)) Borne pi/4 et 0 - Integrale 2*cos(x)*-sin(x)*cos(x) borne Pi:4 et O
I=(V2/2)^3-1 Borne pi/4 et 0 - Integrale 2*cos(x)*-sin(x)*cos(x) borne Pi:4 et O

Cependant je n'arrive pas a primitiver le terme de droite, une petite aide ne serait pas de trop.

Merci de prendre le temps de me répondre.

cos²(x).sin(x) est de la forme - u².u' avec u = cos(x) et donc une primitive est -u³/3

Une primitive de f(x) = cos²(x).sin(x) est F(x) = -(1/3).cos³(x)

...

:zen: