Bonjour à tous!
Je dois travailler sur les intégrales de Wallis mais comme je n'ai pas fait le cours dessus disons que je découvre :doh: ^^
Par hypothèse, (p+2) Wp+2 = (p+1) Wp , de cette relation je devrais ensuite trouver en quoi W2p peut s'écrire de cette façon:
http://fr.wikipedia.org/wiki/Int%C3%A9grales_de_Wallis
Sauf que là je bloque... il y a peut-être quelque chose d'évident qui m'échappe mais je ne vois pas pourquoi W2p = pi/2 * Multiplication de 1 à p de ((2k-1)/2k).
(en sachant que Wo=pi/2 ; et que Wp= intégrale de o à pi/2 de sin^n(t) dt conformément à la définition des intégrales de Wallis)
Pouvez-vous m'éclairer s'il vous plaît? :we:
Merci d'avance!!
Intégrales de Wallis
6 messages
- Page 1 sur 1
Salut,
On montre facilement via une IPP queW_{n+2} = (n+1)W_n) (ce n'est pas par hypothèse ...:s)
(ce n'est pas par hypothèse ...:s)
On a donc une relation de récurrence qui définie chaque terme en fonction de celui 2 rangs avant ...
On détermine facilement et
et 
On peut ainsi déterminer tout les termes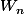 en différenciant le cas n pair du cas n impair.
en différenciant le cas n pair du cas n impair.
Prenons le cas n pair : on pose n = 2p
On sait que
 en remplacant n par 2p
en remplacant n par 2p
Ceci donne donne donc :



...
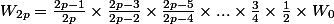
Et finalement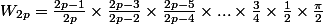
On montre facilement via une IPP que
On a donc une relation de récurrence qui définie chaque terme en fonction de celui 2 rangs avant ...
On détermine facilement
On peut ainsi déterminer tout les termes
Prenons le cas n pair : on pose n = 2p
On sait que
Ceci donne donne donc :
...
Et finalement
Oops je me suis trompée de lien, je voulais seulement afficher l'image:
http://upload.wikimedia.org/math/6/f/6/6f6d2220c6bccf8d80af953df6991fe6.png
Désolée!
http://upload.wikimedia.org/math/6/f/6/6f6d2220c6bccf8d80af953df6991fe6.png
Désolée!
Ok merci beaucoup!! J'ai compris, une fois avoir remplacé n par 2p je me contentais de passer tout de l'autre coté pour trouver W2p, j'avais pas du tout pensé à retrancher "-2" à W2p+2, donc merci beaucoup! :)
Par contre comment j'explique qu'avec (n+2)Wn+2=(n+1)Wn je peux en déduire W2p = pi/2 * Multiplication de 1 à p de ((2k-1)/2k)?
Parce que la série de multiplication que l'on vient d'obtenir n'est pas tout à fait de cette forme là non...?
Par contre comment j'explique qu'avec (n+2)Wn+2=(n+1)Wn je peux en déduire W2p = pi/2 * Multiplication de 1 à p de ((2k-1)/2k)?
Parce que la série de multiplication que l'on vient d'obtenir n'est pas tout à fait de cette forme là non...?
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
