Intégrales

[joridder]

Bjr!
Voici la question sur laquelle je bute (qui est pourtant simple):

soit F:x-> (1/x)* intégrale de (1/(racine(1+t^4)))dt de 0 à x
Montrer que pour tout x>0, 1/(racine(1+x^4)) < F(x)

Merci bcp d'avance!

[tize]

Bonjour,
on pose , .
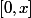
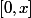
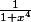
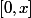
g est continue et dérivable sur et g ' est minorée sur par Inégalité des accroissements finis sur donne :

[joridder]

J'avais pas pensé aux accroisements finis...
Un grand merci!

[joridder]

dans le mm exo
on pose F(0)=1

Montrer que F est continue en 0

J'avais pensé à montrer que lim f en 0 = 1
mais je vois pas comment l montrer

Please help me
Merci :-)

[fahr451]

bonjour

avec les notations de tize

F(x) = [g(x) -g(0)]/(x-0) tend vers g'(0) = 1 quand x ->0

[joridder]

Sacré exo!
J'orai encore besoin de votre aide
J'ai besoin de montrer pour tout u>0,
0<1/(racine(1+u)) - (1-(1/2)u) < (3/8)u²

Un grand merci!

[fahr451]

on pose h(u) = (1+u)^(-1/2)

l'égalité de taylor lagrange donne

il existe c dans ]0,u[

h(u) = h(0) +u h ' (0) +u^2/2 h '' (c)

il reste plus qu ' à calculer h (0), h ' (0) ,h "(c) et de voir que

0 < h " (c) < 3/4

[joridder]

Peut-on en déduire que f admet un dl à l'odre 4 en 0 ?
Lequel?

Muchas gracias :-)

[fahr451]

tu connais les dls usuels ou pas ?
(1+x)^alpha
si oui la question précédente ( avec le 3/8)est sans intérèt