Bonjour , aujourd'hui je souhaiterai obtenir de l'aide sur un exercice sur les Intégrales de Wallis.
J'ai tourné environ 40 minutes en rond , revenant au point de départ à chaque fois.
Tout d'abord j'ai : In = \bigint_{0}^{π/2} cos^n(x) dx et Jn = \bigint_{0}^{π/2} t^2 * cos^n(x)dx
J'ai montrer que In+2 = (n+1)In / (n+2)
Et maintenant je dois montrer que : In+2 = ((n+1)(n+2)Jn - (n+2)^2 Jn+2)/2
Et la je n'arrive pas a simplifier l'expression.
J'ai essayer de travailler d'abord sur Jn+2 , j'ai réussi a sortir l'expression de Jn mais je me retrouve avec un intégrale que je n'arrive pas à mener : Je dois intégré : t^2 * sin^2(x) cos^n(x).
Cordialement.
Ps : Je crois que le symbole de l'intégrale ne fonctionne pas ..
Intégrale de Wallis
10 messages
- Page 1 sur 1
Re: Intégrale de Wallis
par Gisé » 28 Aoû 2016, 22:30
Salut,
Encadre des formules avec les balises LaTeX
Quand on travailles avec des intégrales de Wallis, bien souvent on démontre pas mal de relations avec une IPP.
Encadre des formules avec les balises LaTeX
Quand on travailles avec des intégrales de Wallis, bien souvent on démontre pas mal de relations avec une IPP.
Re: Intégrale de Wallis
par Franc18 » 28 Aoû 2016, 22:42
En fait j'ai essayer les IPP , j'ai du en faire 4 ou 5 et au final je me retrouve avec des expressions qui n'ont aucun rapport avec celle que je cherche
Re: Intégrale de Wallis
par Franc18 » 29 Aoû 2016, 09:33
Je me retrouve donc avec : In = -1/2 *Jn + (n-1) Intégrale ( 0 => Pi/2) (sin(x)^2)*(cos(x))^(n-2)dx ?
Et je dois refaire une IPP ?
Et je dois refaire une IPP ?
Re: Intégrale de Wallis
par Razes » 29 Aoû 2016, 10:14
C'est fini. plus de IPP simplifie et fait apparaitre les
j'aurais du te proposer de calculer
Re: Intégrale de Wallis
par aymanemaysae » 29 Aoû 2016, 10:19
Bonjour,
tout d'abord, je crois que c'est : dx)
et  dx)
si c'est ça, alors on a :
 dx = \int_0^{\frac{\pi}{2}} (x)' \cos^n(x) dx = [x \cos^n(x) ]_0^{\frac{\pi}{2}}+n \int_0^{\frac{\pi}{2}} x \sin(x) \cos^{n-1}(x) dx)
 \cos^{n-1}(x) dx)
: car  ]_0^{\frac{\pi}{2}} = 0)
' \sin(x) \cos^{n-1}(x) dx = n [\frac{x^2}{2} \sin(x) \cos^{n-1}(x)]_0^{\frac{\pi}{2}} - n \int_0^{\frac{\pi}{2}} \frac{x^2}{2} ( \cos^n(x) - (n-1) \sin^2(x) \cos^{n-2}(x)) dx)
 - (n-1) \sin^2(x) \cos^{n-2}(x)) dx)
: car  \cos^{n-1}(x)]_0^{\frac{\pi}{2}} = 0)
 - (n-1) (1-\cos^2(x)) \cos^{n-2}(x)) dx)
 - (n-1) (\cos^{n-2}(x)-\cos^n(x)) ) dx)
 - (n-1) \cos^{n-2}(x)+(n-1)\cos^n(x) ) dx)
 - (n-1) \cos^{n-2}(x) ) dx)
dx + \frac{n(n-1)}{2} \int_0^{\frac{\pi}{2}} x^2 \cos^{n-2}(x)) dx)
}{2} J_{n-2})
ou bien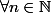
: ^2}{2} J_{n+2} + \frac{(n+2)(n+1)}{2} J_n)
.
Franc18 a écrit:Tout d'abord j'ai : In = \bigint_{0}^{π/2} cos^n(x) dx et Jn = \bigint_{0}^{π/2} t^2 * cos^n(x)dx
tout d'abord, je crois que c'est :
si c'est ça, alors on a :
ou bien
Re: Intégrale de Wallis
par Razes » 29 Aoû 2016, 10:50
@aymanemaysae
Au fait
c'est 
, c'est juste une étourderie dans l'énoncé de Franc18 (merci de l'avoir signalé) et j'ai continué avec. Mais le calcul est bon. Je ne voulais pas faire tout le calcul à la place de Franc18 et je voulais lui en laisser à faire.
Au fait
Re: Intégrale de Wallis
par Franc18 » 29 Aoû 2016, 10:53
Oui en effet désolé de mon erreur d'énoncé. Encore merci pour l'aide , j'ai enfin compris ce qu'il me bloquait.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :