"integrale[?]"
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 01 Aoû 2009, 21:00
par fourize » 01 Aoû 2009, 21:00
bonjour,
profitant de la période estivale pour faire quelque révision, je suis
bloqué sur cette intégrale dont je sollicite votre aide

 = \bigint 3^sqrt{2xt^2+1} dt)
1° calculer la derivée de U(x).
2° calculer l'integrale.
Cordialement,
fourize.
* In God we trust, for all others bring data *
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Aoû 2009, 22:48
par Nightmare » 01 Aoû 2009, 22:48
Salut :happy3:
Le radical est bien en exposant?
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 02 Aoû 2009, 08:36
par MathMoiCa » 02 Aoû 2009, 08:36
Salut,
Déjà as-tu trouvé U'(x) ?
Tu devrais trouver quelque chose de la forme
 \ \Bigint \frac{t^2}{\sqrt{2xt^2+1}} \cdot 3^{\sqrt{2xt^2+1}} \ dt)
Ensuite, il s'agit de trouver une relation entre U' et U et de résoudre l'équadiff...
Pour ce faire, essaie l'intégration par parties dans U', en regardant en particulier quelle est la dérivée de
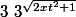
par rapport à t

Pour memo, la dérivée par rapport à x de
})
est
 \ f'(x) \ a^{f(x)})
M.
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 02 Aoû 2009, 09:24
par Epsilon » 02 Aoû 2009, 09:24
bonjour

j'adore les casse-tete :marteau:
MathMoiCa a écrit:Pour memo, la dérivée par rapport à x de
})
est
 \ f'(x) \ a^{f(x)})
M.
la dérivée de U(x) est exacte

 \ \Bigint \frac{t^2}{\sqrt{2xt^2+1}} \cdot 3^{\sqrt{2xt^2+1}} \ dt)
et la dérivée de
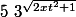
par rapport à t est:
\frac {t}{sqrt(2xt^2+1)}\cdot3^sqrt(2xt^2+1))
donc
=\frac{1}{2} \Bigint 2ln(3) \frac{t}{sqrt(2xt^2+1)}\cdot 3^sqrt(2xt^2+1) \ dt)
genre de h'(x).h(x) ??! mais je vois pas on abouti a quoi ?
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 02 Aoû 2009, 10:07
par MathMoiCa » 02 Aoû 2009, 10:07
Gni ? Ta réécriture de U'(x) (à la dernière ligne) est fausse : où est passé le carré de t ?

Si j'ai dit de considérer la dérivée
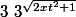
par rapport à t, c'est pour faire une intégration par parties. En effet, en décomposant correctement l'intégrande dans U'(x), on retrouvera facilement la dérivée de
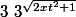
.
Et dans une intégration par parties, on intègre un terme et on en dérive un autre :happy2:
M.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 02 Aoû 2009, 10:27
par Pythales » 02 Aoû 2009, 10:27
Sauf erreur, je trouve
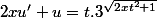
Reste à intégrer ...
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 02 Aoû 2009, 10:59
par MathMoiCa » 02 Aoû 2009, 10:59
Ouais et c'est bien ça le problème :ptdr:
M.
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 02 Aoû 2009, 11:46
par Epsilon » 02 Aoû 2009, 11:46
mathmoica :dodo: oué
=\frac{1}{2} \Bigint t \cdot \frac{2ln(3)t}{sqrt{2xt^2+1}}\cdot 3^sqrt{2xt^2+1} \ dt)
:dodo: :doh: :mur:
moi j'ai trouvé
+U(x)=t\cdot 3^sqrt{2xt^2+1})
?!
d'ou vient le x de Pythales ?
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 02 Aoû 2009, 12:00
par Epsilon » 02 Aoû 2009, 12:00
moi j'ai trouvé
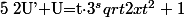
?!
d'ou vient le x de Pythales ?
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 02 Aoû 2009, 15:18
par MathMoiCa » 02 Aoû 2009, 15:18
Epsilon a écrit:mathmoica :dodo: oué
=\frac{1}{2} \Bigint t \cdot \frac{2ln(3)t}{sqrt{2xt^2+1}}\cdot 3^sqrt{2xt^2+1} \ dt)
:dodo: :doh: :mur:
moi j'ai trouvé
+U(x)=t\cdot 3^sqrt{2xt^2+1})
?!
d'ou vient le x de Pythales ?
La dérivée par rapport à t donne un facteur x :
Dérivée de
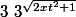
par rapport à t est
 xt}{\sqrt{2xt^2+1}} \cdot 3^{\sqrt{2xt^2+1}})
Donc lors de l'intégration par parties, on a :
 xt}{\sqrt{2xt^2+1}}\cdot 3^{\sqrt{2xt^2+1}} \ dt)
Et donc :
=\frac{1}{2x}\left(t 3^{\sqrt{2xt^2+1}}-\Bigint 3^{\sqrt{2xt^2+1}} \ dt\right))
Ce qui donne la relation obtenue par Pythalès.
M.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 02 Aoû 2009, 23:52
par xyz1975 » 02 Aoû 2009, 23:52
Je ne comprends pas comment vous dérivez sous le signe intégrale sans au moins justifier ce passage, tout ce que j'ai vu est un calcul formel.
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 03 Aoû 2009, 08:30
par MathMoiCa » 03 Aoû 2009, 08:30
xyz1975 a écrit:Je ne comprends pas comment vous dérivez sous le signe intégrale sans au moins justifier ce passage, tout ce que j'ai vu est un calcul formel.
Ça, c'est laissé à l'appréciation de fourize : c'est une application du cours

M.
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 03 Aoû 2009, 12:10
par prody-G » 03 Aoû 2009, 12:10
de toute façon ils peuvent pas le justifier puisque fourize n'a pas donné les bornes, on sait pas sur quel intervalle on intègre et si c'est bien défini =D
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 03 Aoû 2009, 14:52
par MathMoiCa » 03 Aoû 2009, 14:52
Aaaah ouais xD
dans ce cas, ce n'est pas très important, non ? Il s'agit juste d'une primitive :marteau:
dsl, mais les justifications de ce genre et moi, ça fait deux ^^
M.

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 03 Aoû 2009, 19:07
par fourize » 03 Aoû 2009, 19:07
bonsoir,
déjà merci à tous pour l'importance que vous accordez cette fois à mon sujet :-)
pour commencer:
* la justification de la dérivée avec le signe intégrale est, effectivement comme disait un de nos amis, pas nécessaire puisqu'il s'agit de primitive I.e dans le domaine convenable.
* pour ce qu'il est de la dérivée: j'hésitais entre dérivée par rapport à x ou t. bien que vous me rassurer qu'il faut dériver par rapport à x. ne faut il pas justifier (ou poser des conditions éventuelle) pour t ???
* pour cette primitive ? ce qui me gene le plus ce que u est en fonction de x, et on resoud l'équation par rapport à t :triste: je suis perdu !
_ est que faire u'(x) + u(x) =0 peut me méner à quelque chose ??
cordialement;
fourize.
* In God we trust, for all others bring data *
 par alavacommejetepousse » 03 Aoû 2009, 20:55
par alavacommejetepousse » 03 Aoû 2009, 20:55
bonsoir puisque j'ai compris que ce n'était pas une intégrale, pour y voir plus clair il semblerait naturel de considérer une fonction de deux variables et des dérivées partielles
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 04 Aoû 2009, 10:10
par prody-G » 04 Aoû 2009, 10:10
fourize a écrit:bonsoir,
déjà merci à tous pour l'importance que vous accordez cette fois à mon sujet

pour commencer:
* la justification de la dérivée avec le signe intégrale est, effectivement comme disait un de nos amis, pas nécessaire puisqu'il s'agit de primitive I.e dans le domaine convenable.
* pour ce qu'il est de la dérivée: j'hésitais entre dérivée par rapport à x ou t. bien que vous me rassurer qu'il faut dériver par rapport à x. ne faut il pas justifier (ou poser des conditions éventuelle) pour t ???
* pour cette primitive ? ce qui me gene le plus ce que u est en fonction de x, et on resoud l'équation par rapport à t :triste: je suis perdu !
_ est que faire u'(x) + u(x) =0 peut me méner à quelque chose ??
cordialement;
fourize.
une petite contradiction dans ce que tu viens de dire ^^'.
Tu dis que le domaine est convenable mais tu demandes s'il faut poser des conditions sur t alors que c'est la variable d'intégration (ie qui balaie ton domaine).
Il faudrait connaître les bornes pour pouvoir justifier, l'existence de la racine carrée d'une part, puis l'intégrabilité de la fonction de t (d'où la remarque de xyz1975). Par exemple, ça change tout si l'une des bornes est x ou bien l'infini.
Non on ne résout pas par rapport à t mais justement par rapport à x. Les seules opérations que l'on a faite sur t c'était dans le cadre de l'intégration.
Oui l'équation 2xu'(x)+u(x)=0 te donne une solution de l'équation sans second membre, mais la variation de la constante est quand même bien difficile dans ce cas là ^^'.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Aoû 2009, 15:02
par Nightmare » 04 Aoû 2009, 15:02
Salut à tous !
J'arrive un peu en plein milieu de la bataille mais j'avouerai ne pas comprendre ce qui bloque pour finir.
L'intégration de l'équadiff obtenue ne me semble pas si insurmontable.
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 04 Aoû 2009, 18:14
par prody-G » 04 Aoû 2009, 18:14
Si on suppose qu'on intègre entre 0 et 1 pour simplifier.
Une solution de l'ESSM est
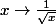
.
Si
=\frac{C(x)}{\sqrt x })
, je tombe sur un truc de la forme :
=\frac{1}{2}\frac{3^{\sqrt{2x+1}}}{\sqrt x })
et je t'avoue que j'ai du mal à intégrer ça ^^'.
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 04 Aoû 2009, 18:20
par MathMoiCa » 04 Aoû 2009, 18:20
Nightmare a écrit:Salut à tous !
J'arrive un peu en plein milieu de la bataille mais j'avouerai ne pas comprendre ce qui bloque pour finir.
L'intégration de l'équadiff obtenue ne me semble pas si insurmontable.
Si tu arrives à intégrer le second membre (par rapport à x), fais-nous part de ta méthode :zen:
M.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités