Intégrale du sinus cardinal...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
 par Als128 » 01 Nov 2009, 11:51
par Als128 » 01 Nov 2009, 11:51
Bonjour à tous,
toujours dans ma (recon)quête des mathématiques après la prépa, j'ai un petit problème avec le calcul d'une intégrale...
Voilà c'est un exercice en 4 question et je bloque sur la dernière.
On pose
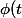=\int_{0}^{\infty}\frac{sin(u)}{u}e^{-tu}du)
avec

Les 3 premières questions sont du cours et du calcul pour démontrer
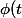=Arctan(t) + \frac{\pi}{2})
et la je bloque sur la dernière :
On définit la suite
))
par
) = \int_{0}^{n}\frac{sin(u)}{u}e^{-tu}du)
Montrer que

tend vers

uniformément quand n tnd vers

. En déduire la valeur de
}{u})
Même si je me doute que le resultat de l'intégrale du sin cardinal sera

, je vois pas bien comment partir pour démontrer la convergence uniforme
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 01 Nov 2009, 12:13
par ffpower » 01 Nov 2009, 12:13
Bonjour.Je n ai pas fait les calculs,mais je pense qu on doit pouvoir s en sortir en faisant une integration par partie.On primitive le sinus cardinal,on derive l exponentielle,ce qui va sortir un t devant l integrale,et apres on sépare les cas t petit et t grand. Tout ceci est a vérifier bien sur..
 par alavacommejetepousse » 01 Nov 2009, 12:17
par alavacommejetepousse » 01 Nov 2009, 12:17
bonjour uniformément sur quoi? R+? ou [a,+infini[ a>0 ?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 01 Nov 2009, 12:19
par ffpower » 01 Nov 2009, 12:19
R+ a mon avis,sinon je vois pas comment on pourrait conclure apres
-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
 par Als128 » 01 Nov 2009, 12:31
par Als128 » 01 Nov 2009, 12:31
Alors je vous assure que l'énoncé ne précise rien de plus... (c'est la copie exacte de la 4ème question)
Quand à la solution proposée par le livre, elle est incompréhensible car succinte et mal expliquée : elle propose d'appliquer le lemme d'Abel avec les fonctions

et
)
. Pour avoir regardé sur wiki, j'arrive pas à trouver une application du lemme d'Abel dans un cas autre que les series entières...
Bref, je nage complet et je suis ravir de vous avoir pour m'aider :we:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 01 Nov 2009, 13:21
par Joker62 » 01 Nov 2009, 13:21
Haileau ;)
Le critère d'Abel pour les intégrales généralisée sur un domaine de la forme [a;+;)[ assure que si on a une intégrande de la forme f(x)g(x) avec f décroissante positive qui tend vers 0 et que l'intégrale de g sur tout intervalle de la forme [a;k] existe et est bornée alors l'intégrale initiale converge.
Ici pour montrer la convergence uniforme sur le domaine en question ( je ne me prononce pas sur ça :D) fait la différence des deux, tu vas te retrouver avec une intégrale sur [n;+;)[ et la le lemme d'Abel peut s'appliquer.
Maintenant reste à prouver que ça tend vers 0.
-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
 par Als128 » 01 Nov 2009, 13:58
par Als128 » 01 Nov 2009, 13:58
C'est bon !!!
Merci beaucoup... En fait mon cours est trop mal agencé, c'est incompréhensible pour quelqu'un qui reprend ses études.. En plus, les fasicules sont modernes, l'impression date de 1989...
L'aide de ce forum est très appréciable. Merci encore une fois
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
