Integrale au sens de lebesgue

[joanie58]

Bonjour,

je dois calculer l'intégrale au sens de Lebesgue sur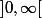 de la fonction suivante

[barbu23]

Bonsoir, :happy3:

Pourquoi : ?

Cordialement. :happy3:

[mrif]

Bonsoir, :happy3:

Pourquoi : ?

Cordialement. :happy3:

Je suppose que la fonction f est définie par: , autrement l'intégrale vaut trivialement + l'infini.

[barbu23]

Je suppose que la fonction f est définie par: , autrement l'intégrale vaut trivialement + l'infini.

Oui, c'est ce que je pense. Merci. :we:
On attend la confirmation de joanie58. :happy3:
Cordialement. :happy3:

[Ben314]

Salut,
Tu es... à peu prés sur la bonne voie, sauf que :

1) Elles sont "bizarres" tes notations :
- Pourquoi ton premier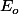 tu ne l'appelle pas directement
- Pourquoi as-tu, a la ligne d'en dessous, une définition différente (à savoir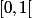 ) pour le même ensemble ?

2) Lorsque tu écrit , ça se réfère auquel de tes deux 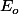? Parce que, vu le début de la ligne, il me semblait que ça se référait à celui des deux qui est égal à , sauf que celui là il est pas de mesure nulle, non ?

3) Tu écrit que : ça me parait plus que douteux si on ne fait aucune hypothèse particulière concernan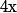t le et le de cette formule.
Et, si, par hasard, on fait l'hypothèse que alors il n'y a rien à encadrer du tout vu que dans ce cas là, on a donc

[mrif]

Bonjour,

je dois calculer l'intégrale au sens de Lebesgue sur de la fonction suivante



où est la partie entière de x

----------------------------------------------------------------------------------------------------------
voici ce que j'ai fait

soit


=>
=>

mais ensuite je suis un peu bloqué....
est-ce que je suis sur la bonne voie où bien je n'ai pas besoin de faire cela...

pouvez-vous m'aider
merci

Comme j'ai précisé précédemment, je pense qu'il y a une rreur dans la définition de f.
Une manière simple de répondre est de remarquer que tu es en présence d'une fonction étagèe prenant les valeurs:
Si on pose , la mesure de est égale à 1 pour tout n.
L'intégrale de cette fonction étagée est donc égale à , somme facile à calculer comme somme des termes d'une suite géométrique.

Edit: La fonction n'est pas étagée puisqu'elle ne prend pas un nombre fini de valeurs, mais la démo reste valable.

[joanie58]

Comme j'ai précisé précédemment, je pense qu'il y a une rreur dans la définition de f.
Une manière simple de répondre est de remarquer que tu es en présence d'une fonction étagèe prenant les valeurs:
Si on pose , la mesure de est égale à 1 pour tout n.
L'intégrale de cette fonction étagée est donc égale à , somme facile à calculer comme somme des termes d'une suite géométrique.

Edit: La fonction n'est pas étagée puisqu'elle ne prend pas un nombre fini de valeurs, mais la démo reste valable.

oooo c'est super simple finalement!

Dans le fond j'ai



on a alors

c'est tout....?

[Ben314]

Qui a dit que c'était compliqué ? :zen:

[joanie58]

alalal je vois toujours les questions pire qu'elles le sont vraiment! :triste:
Merci pour votre aide! :)