Intégrale par décomposition en éléments simples

par **Muze** » 15 Aoû 2006, 21:58

Voilà alors j'ai un problème avec cette intégrale... je vous la mets ainsi que mon raisonnement :

Calculer l'intégrale

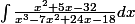
Voici mon raisonnement :

1) j'ai cherché les racines évidentes du dénominateur : c'est 1.
J'ai donc divisé le dénominateur par x-1 ce qui me fait

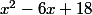
comme résultat de la division
L'intégrale devient :

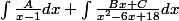
J'ai donc

2)En développant le numérateur j'arrive à ça :

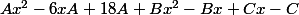
Et donc on se rapportant à la donnée on a :
(1)

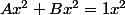
(2)

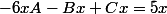
(3)

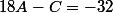
donc A+B=1
-6A-B+C=5
18A-C=-32

Alors là impossible de me sortir de ces équations, j'ai sûrement du faire une faute quelque part... quelqu'un aurait une idée? :mur:

par **nekros** » 15 Aoû 2006, 22:26

Salut,

En additionnant les deux dernières lignes, tu trouves une nouvelle équation sans C.

Avec la première, tu en déduis A et B.

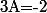
et

Enfin, tu en déduis

Sauf erreurs.

A+

par **Muze** » 15 Aoû 2006, 22:27

J'suis vraiment bête...
Merci beaucoup, normalement mon intégrale devrait jouer... merci 1000 fois j'arrive à faire les trucs supers compliqués mais quand il s'agit de faire des trucs simples, j'suis plus là :marteau:

par **nekros** » 15 Aoû 2006, 22:29

De rien :id:

A+

par **Muze** » 15 Aoû 2006, 22:36

Par contre je trouve pas la même chose...
Si on additionne les deux dernières équations on trouve
12a-b=-27
en tenant compte du fait que a=-b+1
je remplace et ca me donne 12(-b+1)-b=-27
ce qui fait -12b+12-b=-27 donc -13b=-39

j'ai donc b=3, ensuite a=-2 et c=-4 et ca marche... bizarre

par **nekros** » 15 Aoû 2006, 22:45

On aurait du utiliser les formules de Cramer.

Le déterminant du système vaut

.

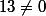
Donc le système admet une unique solution.

Avec les formules de Cramer, je retrouve bien les solutions que je t'avais donné.

A+

par **nada-top** » 15 Aoû 2006, 23:18

j'ai donc b=3, ensuite a=-2 et c=-4 et ca marche... bizarre

:doh: elles sont bel et bien les solutions Nekros , peut etre j'ai pas suis l'exo mais là vraiment je comprends rien.

On aurait du utiliser les formules de Cramer.

c'est pas si compliqué pour avoir recours à Cramer je crois.

par **nekros** » 15 Aoû 2006, 23:19

>Nada-Top => simplifie mes solutions pour voir :ptdr:

(désolé)

A+

par **Nightmare** » 15 Aoû 2006, 23:25

Bonsoir

Pourquoi se compliquer la vie à résoudre un système ? :lol3:

En mutlipliant par x-1 :

Avec x=1 :

En multipliant par x :

En passant à la limite en +oo :

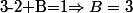
Il suffit ensuite de prendre x quelconque pour trouver C

:happy3:

par **nekros** » 15 Aoû 2006, 23:34

Oui Nightmare, on trouve bien les mêmes solutions :

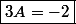
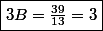
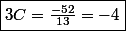
A+

par **nekros** » 15 Aoû 2006, 23:35

Comme quoi ne pas simplifier peut prêter à confusion :ptdr: :ptdr:

par **nada-top** » 15 Aoû 2006, 23:57

nada-top a écrit:elles sont bel et bien les solutions de Nekros , peut etre j'ai pas suis l'exo mais là vraiment je comprends rien.

non Nekros tu m'as pas bien compris (j'ai oublié de dans ma phrase) :ptdr: ..d'ailleurs c'est de là ou viens mon étonnement car je vois les memes solutions et je voyais pas de bizarre.

Muze a écrit:j'ai donc b=3, ensuite a=-2 et c=-4 et ca marche... bizarre

Nekros a écrit:>Nada-Top => simplifie mes solutions pour voir

(désolé)

je suis pas si bete quand meme :lol4:

par **nekros** » 16 Aoû 2006, 00:03

nada-top a écrit:non Nekros tu m'as pas bien compris (j'ai oublié de dans ma phrase) :ptdr: ..d'ailleurs c'est de là ou viens mon étonnement car je vois les memes solutions et je voyais pas de bizarre.

Tout s'explique maintenant :ptdr:

je suis pas si bete quand meme :lol4:

Désolé, loin de moi cette idée. :cry:

A+

par **nada-top** » 16 Aoû 2006, 00:08

ça fait rien d'ailleurs c'est ma phrase qui a amené au sens inverse sans ce "de" :ptdr:

@+

par **Muze** » 16 Aoû 2006, 10:00

Bon ce dont vous me parlez avec Kramer, j'ai pas appris... Mais pourtant mes solutions marchent...

par **Muze** » 16 Aoû 2006, 10:01

J'avais pas réalisé qu'on avait trouvé la même chose :zen:

par **nada-top** » 16 Aoû 2006, 10:44

Bonjour Muze,
tu peux regarder ici un petit résumé pour les formules du systeme Cramer.(post n° 9)
@+

par **Muze** » 16 Aoû 2006, 11:48

Ah, merci...
C'est marrant comme vos programmes sont complètement différents des notres... Je suis en polytechnique et on n'a pas du tout vu ca... (bon aussi en chimie, je pense que si j'avais été en maths je l'aurais vu)
Aller aujourd'hui j'attaque les intégrales curvilignes :happy2:

par **nada-top** » 16 Aoû 2006, 12:40

de rein :jap:

Intégrale par décomposition en éléments simples

Intégrale par décomposition en éléments simples

Qui est en ligne