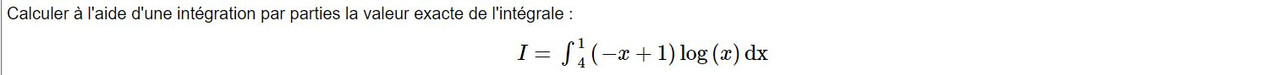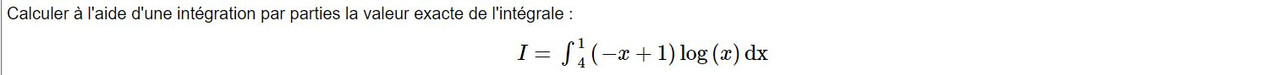Integral_ln(x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Liam20
- Membre Relatif
- Messages: 110
- Enregistré le: 26 Oct 2020, 14:07
-
 par Liam20 » 23 Mai 2022, 13:52
par Liam20 » 23 Mai 2022, 13:52
Bonjour j'ai une question sur cet exercice , Est ce que il a y une erreur sur log(x) ou pas ?
Je ne comprends pas la solution pourquoi v(x) = log(x) et v'(x) = 1/x normale ce n'est pas vraie ? car integrale log(x) = xlnx-x !

-
Black Jack
 par Black Jack » 23 Mai 2022, 14:32
par Black Jack » 23 Mai 2022, 14:32
Bonjour,
Je ne comprends pas ce qui te tracasse.
La solution donnée est correcte.
*******
Et on a bien : v(x) = ln(x) et v'(x) = 1/x
et on a bien aussi (x.ln(x) - x) est une primitive de ln(x)
D'ailleurs en dérivant (x.ln(x) - x) ... on retrouve bien ln(x)
(x.ln(x) + x)' = ln(x) + x/x - 1 = ln(x)
Je ne vois aucun problème là dedans.

-
Liam20
- Membre Relatif
- Messages: 110
- Enregistré le: 26 Oct 2020, 14:07
-
 par Liam20 » 23 Mai 2022, 14:47
par Liam20 » 23 Mai 2022, 14:47
Merci bcp , désolé c'est moi qui a trompé
en fait je suis trompé v'(x) est primitive donc ce n'est pas primitive c'est la dérivé le v(x) = ln(x)

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Mai 2022, 18:52
par Sa Majesté » 23 Mai 2022, 18:52
Petite remarque : généralement on simplifie ln(4) par 2ln(2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités