1^infini
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 18 Oct 2012, 21:50
par Kimou » 18 Oct 2012, 21:50
Bonjour
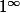
est une forme indéterminée, car on en supposant qu'on ne suive pas notre instinct de dire que ca vaut 1 on retombe toujours sur une forme indéterminée. De plus on sait que la limite lorque n tend vers l'inifini de
^n)
tend vers

.
Mais que pensez vous de cette démo:
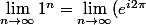^n<br />=\lim_{n \to \infty} (e^{ni2\pi})<br />=\lim_{n \to \infty} (cos(2n\pi) + isin(2n\pi))<br />=1)
Non?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 18 Oct 2012, 21:53
par Kikoo <3 Bieber » 18 Oct 2012, 21:53
Kimou a écrit:Bonjour
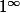
est une forme indéterminée, car on en supposant qu'on ne suive pas notre instinct de dire que ca vaut 1 on retombe toujours sur une forme indéterminée. De plus on sait que la limite lorque n tend vers l'inifini de
^n)
tend vers

.
Mais que pensez vous de cette démo:
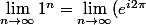^n<br />=\lim_{n \to \infty} (e^{ni2\pi})<br />=\lim_{n \to \infty} (cos(2n\pi) + isin(2n\pi))<br />=1 non?)
Yo,
Where is la démo ? Ce que je vois c'est que tu aboutis sur une forme bizarre à la fin qui ne te permet pas de conclure.

vaudra toujours 1 quand x est positif. Il n'y a aucune forme indéterminée puisqu'il s'agit d'une égalité.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 18 Oct 2012, 21:55
par Kimou » 18 Oct 2012, 21:55
Kikoo <3 Bieber a écrit:Yo,
Where is la démo ? Ce que je vois c'est que tu aboutis sur une forme bizarre à la fin qui ne te permet pas de conclure.

vaudra toujours 1 quand x est positif. Il n'y a aucune forme indéterminée puisqu'il s'agit d'une égalité.
Une forme bizarre? Je ne vois aucune forme bizarre mais plutot quelque chose qui au contraire permet de conclure de maniere évidente. Quant à la forme indéterminée, va revoir le cours, je t'assure que s'en est une, même si elle nous parait folle

la limite de du cosinus etant 1 et la limite du sinus étant 0 évidemment
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Oct 2012, 21:55
par Nightmare » 18 Oct 2012, 21:55
Hello,
1^infini est une forme indéterminée veut dire qu'on a pas de résultat général pour la limite de f(x)^g(x) lorsque f(x) tend vers 1 et g(x) tend vers +oo, cela étant, ça n'empêche pas que la suite 1^n ou plus généralement les suite 1^(g(n)) où g(n) tend vers +oo sont toutes constantes égales à 1 et en particulier convergent vers 1.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 18 Oct 2012, 22:01
par Kimou » 18 Oct 2012, 22:01
Nightmare a écrit:Hello,
1^infini est une forme indéterminée veut dire qu'on a pas de résultat général pour la limite de f(x)^g(x) lorsque f(x) tend vers 1 et g(x) tend vers +oo, cela étant, ça n'empêche pas que la suite 1^n ou plus généralement les suite 1^(g(n)) où g(n) tend vers +oo sont toutes constantes égales à 1 et en particulier convergent vers 1.
salut
Tout aussi bête que cela y parait ce n'est pas si simple apparemment. Des sites web relate la chose en disant simplement que 1 multiplié par lui-même un nombre de fois infini donne une forme indéterminée...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Oct 2012, 22:03
par Nightmare » 18 Oct 2012, 22:03
1^(n'importe quoi) sera toujours égal à 1 (modulo quelques restrictions sur "n'importe quoi" pour que ça ait un sens de le mettre en exposant).
Donc 1^n=1 quelque soit n et en particulier (1^n) converge vers 1.
Par contre, on ne peut généralement rien dire de la limite d'une suite sous la forme (u(n))^(v(n)) où u(n) tend vers 1 et v(n) tend vers l'infini.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 18 Oct 2012, 22:08
par Kikoo <3 Bieber » 18 Oct 2012, 22:08
Ah ben finalement, c'était pas si évident que ça en effet ;)
Mais en ce qui concerne le simple 1 puissance quelque chose, quelqu'un pour me dire si 1^infini donne 1 ?
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 18 Oct 2012, 22:09
par Kimou » 18 Oct 2012, 22:09
Nightmare a écrit:1^(n'importe quoi) sera toujours égal à 1 (modulo quelques restrictions sur "n'importe quoi" pour que ça ait un sens de le mettre en exposant).
Donc 1^n=1 quelque soit n et en particulier (1^n) converge vers 1.
Par contre, on ne peut généralement rien dire de la limite d'une suite sous la forme (u(n))^(v(n)) où u(n) tend vers 1 et v(n) tend vers l'infini.
Je suis d'accord a priori.
Mais pour la petite histoire je suis en master de maths et ma soeur (en prépa) a dans son cahier de cours exactement ce que j'ai mis au dessus avec exemple: lim 1^n forme indéterminée on ne peut pas conclure.
Puis je suis tombé sur ce site:
http://villemin.gerard.free.fr/aMaths/Analyse/Limite/UnPinfin.htm qui me met quelque doute... Donc je cherchais une façon de les faire "mentir" ^^
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Oct 2012, 22:14
par Nightmare » 18 Oct 2012, 22:14
Personne ne se contredit réellement, c'est juste une question de notation.
Quand on dit que 1^(infini) est indéterminée, on ne sous-entend pas que lim 1^(un truc qui tend vers l'infini) est indéterminée mais que lim (un truc qui tend vers 1)^(un truc qui tend vers l'infini) est indéterminée.
Maintenant, on peut aussi parler de la forme 1^(infini) qui là désigne quelque chose de la forme lim 1^(un truc qui tend vers l'infini) et ça ça sera toujours égal à 1 (encore une fois pourvu que ce soit bien défini dans R). Il n'y a rien d'autre à dire pour le démontrer que 1^(machin)=1 quel que soit machin, donc la suite est constante.
Pour finir, on peut aussi noter 1^(infini)
un produit infini du type

où I est un ensemble de cardinal infini, mais ceci est aussi non défini.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 18 Oct 2012, 22:19
par Kikoo <3 Bieber » 18 Oct 2012, 22:19
Nightmare a écrit:Personne ne se contredit réellement, c'est juste une question de notation.
Quand on dit que 1^(infini) est indéterminée, on ne sous-entend pas que lim 1^(un truc qui tend vers l'infini) est indéterminée mais que lim (un truc qui tend vers 1)^(un truc qui tend vers l'infini) est indéterminée.
Merci, c'est ce qu'il me semblait en effet

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
est une forme indéterminée, car on en supposant qu'on ne suive pas notre instinct de dire que ca vaut 1 on retombe toujours sur une forme indéterminée. De plus on sait que la limite lorque n tend vers l'inifini de
tend vers
.
vaudra toujours 1 quand x est positif. Il n'y a aucune forme indéterminée puisqu'il s'agit d'une égalité.