Inegalite

[pandad]

Je n'arrive pas a resoudre cette inegalite :

a+b-2*radical(a*b)<a-b

Povez vous me donner une idee?

[Ben314]

Salut,
Objectif évident : virer la méchante racine carrée pour se ramener à un gentil polynôme.

Méthode 1 : si


Méthode 2 : (en supposant que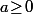 et )
Poser et

[MMu]

Je n'arrive pas a resoudre cette inegalite :

a+b-2*radical(a*b)<a-b

Povez vous me donner une idee?

Ce n'est pas vrai si par ex ..

[zygomatique]

salut

on ne sait pas où vivent a et b mais déjà il est nécessaire qu'ils aient même signe pour assurer l'existence des objets écrits ....

ensuite on peut tout de même simplifier ::



évidemment si a et b sont positifs on veut donc

et si a et b sont négatifs on veut donc

on peut même conclure directement dans ce dernier cas .... connaissant les propriétés de la fonction racine carrée ....

[chan79]

salut
dans le cas et , l'inégalité est toujours vraie

vois si