Inégalité et puissance de somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
salouet
- Messages: 3
- Enregistré le: 01 Oct 2012, 09:34
-
 par salouet » 01 Oct 2012, 09:48
par salouet » 01 Oct 2012, 09:48
Bonjour
aidez moi svp à démontrer cet inégalité
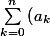 ^{\alpha }\leq \frac{1}{\alpha } \left( \sum\limits_{k=0}^{n}a_{k}\right) ^{\alpha })
avec
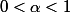
et

réels positifs
j'ai essayé la récurrence, l'inégalité de Jensen....., main en vain :mur:
Merci d'avance
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 10:03
par arnaud32 » 01 Oct 2012, 10:03
prend alph=1/2 et a_k=1 pour tout k, ca te donne quoi?
-
salouet
- Messages: 3
- Enregistré le: 01 Oct 2012, 09:34
-
 par salouet » 01 Oct 2012, 10:19
par salouet » 01 Oct 2012, 10:19
arnaud32 a écrit:prend alph=1/2 et a_k=1 pour tout k, ca te donne quoi?
si n=8 (exemple ) ça donne 9<6 donc cette inégalité n'est pas toujours vrai
est il possible qu'elle soit vérifiée pour certaines restrictions sur a_k?
merci
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 01 Oct 2012, 10:45
par arnaud32 » 01 Oct 2012, 10:45
tu notes
)
et
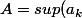)
tu supposes a>0
on iengalite va te donner
a^{\alpha}\leq \frac{((n+1)A)^{\alpha}}{\alpha})
et donc
^{1-\alpha}\leq \frac{A^{\alpha}}{\alpha a^{\alpha}})
-
salouet
- Messages: 3
- Enregistré le: 01 Oct 2012, 09:34
-
 par salouet » 01 Oct 2012, 11:08
par salouet » 01 Oct 2012, 11:08
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités