Inégalité factorielle

par **Kyg** » 17 Sep 2015, 14:14

Bonjour,

Je n'arrive pas à démontrer que pour tout

par **Monsieur23** » 17 Sep 2015, 14:21

Aloha,

En écrivant tout, c'est assez facile

Tu as ton égalité termes à termes, donc ça reste ok pour le produit.

par **Kyg** » 17 Sep 2015, 14:28

Merci beaucoup mais comment rédiger une réponse de manière peut être plus rigoureuse à partir de ça ?

par **alphamethyste** » 17 Sep 2015, 14:33

Kyg a écrit:Bonjour,

Je n'arrive pas à démontrer que pour tout

dans

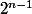
alors 2 est mis n-1 fois en facteur:
2.2 etc ... n-1 fois

tandis que dans n! on fait un produit de n-1 facteurs supérieurs ou égal à 2 :
2.3...n

de sorte que

ensuite pour l'autre

dans n! on fait un produit de n-1 facteurs inferieur ou égal à n :

tandis que dans n^n c'est un produit de n facteurs de valeur n

par **Monsieur23** » 17 Sep 2015, 14:57

Kyg a écrit:Merci beaucoup mais comment rédiger une réponse de manière peut être plus rigoureuse à partir de ça ?

Tu as

et

,
et pour tout

,

, donc

Tu peux faire pareil pour l'autre, en ajoutant

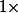
au début de la factorielle, pour faire autant de termes dans le produit que n^n.

par **Kyg** » 17 Sep 2015, 17:27

Oh d'accord, merci énormément pour votre aide !

par **zygomatique** » 17 Sep 2015, 18:38

salut

par récurrence ....

dès que n > 0

...

:lol3:

Inégalité factorielle

Inégalité factorielle

Qui est en ligne